题目内容
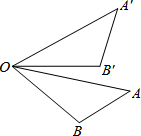如图，若将△AOB绕点O按逆时针方向旋转44°后，得到△A′OB′，且AO=2，则AA′的长为（ ）| A、4sin22° |
| B、2sin44° |
| C、4cos22° |
| D、2cos44° |
考点：旋转的性质
专题：
分析：如图，作辅助线；由题意得OA=OA′=2，∠AOA′=44°；证明∠A′OC=∠AOC=22°，A′C=AC；由正弦函数的定义求出A′C的长度，即可解决问题．
解答：
解：如图，连接AA′，过点O作OC⊥AA′；
由题意得：OA=OA′=2，∠AOA′=44°，
∴∠A′OC=∠AOC=22°，A′C=AC；
∵sin22°=
，
∴A′C=2sin22°，AA′=2A′C=4sin22°，
故选A．
解：如图，连接AA′，过点O作OC⊥AA′；由题意得：OA=OA′=2，∠AOA′=44°，
∴∠A′OC=∠AOC=22°，A′C=AC；
∵sin22°=
| A′C |
| A′O |
∴A′C=2sin22°，AA′=2A′C=4sin22°，
故选A．
点评：该题主要考查了旋转变换的性质及其应用问题；解题的关键是作辅助线，灵活运用等腰三角形的性质、三角函数的定义来分析、判断、解答．
练习册系列答案
相关题目
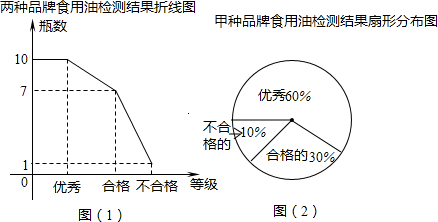
如图，两双曲线y=根据信息，下列判断：①甲、乙两种品牌食用油被抽取的18瓶中只有1瓶检测为“不合格”；②甲种品牌食用油被抽取了10瓶用于检测；③在该超市购买一瓶乙品牌食用油，估计能买到“优秀”等级的概率是
；其中正确的是（ ）
| 1 |
| 2 |
| A、只有①② | B、只有①③ |
| C、只有②③ | D、①②③ |
如图所示，在?ABCD中，对角线AC与BD相交于点O，过点O任作一条直线分别交AB、CD于点E、F．已知△ABC的三边长分别为4、6、8，与它相似的△DEF的最短边长为6，则△DEF的最长边的长为（ ）
| A、8 | B、12 | C、10 | D、9 |
“五•一”节，某超市开展“有奖促销”活动，凡购物不少于30元的顾客均有一次转动转盘的机会（如图，转盘被分为8个全等的小扇形），当指针最终指向数字8时，该顾客获一等奖；当指针最终指向3或5时，该顾客获二等奖（若指针指向分界线则重转）． 经统计，当天发放一、二等奖奖品共600份，那么据此估计参与此次活动的顾客为
如图，这是一张2×3的正方形网格图，A、B、C都是格点，求证：∠ABC=45°．