题目内容
已知△ABC的三边长分别为4、6、8,与它相似的△DEF的最短边长为6,则△DEF的最长边的长为( )
| A、8 | B、12 | C、10 | D、9 |
考点:相似三角形的性质
专题:
分析:根据△ABC∽△DEF,根据相似三角形的对应边成比例,即可得4:6=8:x,则可求得最长边的边长.
解答:解:∵△ABC的三边长分别为4、6、8,与它相似的△DEF的最短边长为6,
∴4:6=8:x,
解得:x=12,
则△DEF的最长边的长为12.
故选:B.
∴4:6=8:x,
解得:x=12,
则△DEF的最长边的长为12.
故选:B.
点评:此题考查了相似三角形的性质.解题的关键是注意相似三角形的对应边成比例定理的应用.

练习册系列答案
相关题目
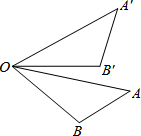 如图,若将△AOB绕点O按逆时针方向旋转44°后,得到△A′OB′,且AO=2,则AA′的长为( )
如图,若将△AOB绕点O按逆时针方向旋转44°后,得到△A′OB′,且AO=2,则AA′的长为( )| A、4sin22° |
| B、2sin44° |
| C、4cos22° |
| D、2cos44° |
 如图所示,OB=1,OC=3,AB=AC=4,求点A的坐标.
如图所示,OB=1,OC=3,AB=AC=4,求点A的坐标. 如图,△ABD是等腰直角三角形,∠BAD=90°,BC∥AD,BC=2AB,CE平分∠BCD,交AB于E,交BD于H.求证:
如图,△ABD是等腰直角三角形,∠BAD=90°,BC∥AD,BC=2AB,CE平分∠BCD,交AB于E,交BD于H.求证: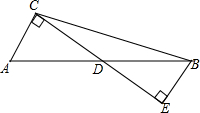 如图,D是AB的中点,CE过点D且AC⊥CE于C,BE⊥CE于E,已知sin∠BCD=
如图,D是AB的中点,CE过点D且AC⊥CE于C,BE⊥CE于E,已知sin∠BCD= 该几何体最少由多少个小立方体组成?最多由多少个小立方体组成.
该几何体最少由多少个小立方体组成?最多由多少个小立方体组成.