题目内容
 如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,交AC于点G.
如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,交AC于点G.(1)求证:AD=DI.
(2)探究线段ID,DG,DB之间的数量关系,并证明.
(3)若AC=4,BC=3,求AD的长.
(4)在(3)的条件下,求DG及AG的长.
考点:圆的综合题
专题:综合题
分析:(1)连接AI,如图1,由点I是△ABC的内心可得∠BAI=∠CAI,∠ABI=∠CBI,根据圆周角定理可得∠DAC=∠DBC,从而可得∠ABI=∠DAC,然后利用外角性质即可解决问题;
(2)易证△DAG∽△DBA,根据相似三角形的性质可得AD2=DG•DB,由AD=ID即可得到ID2=DG•DB;
(3)过点D作DE⊥AB于E,过点D作DF⊥BC于F,连接DC,如图2.根据勾股定理可得AB=5,易证△BED≌△BFD,则有DE=DF,BE=BF.由∠ABD=∠CBD可得DA=DC,然后根据勾股定理证到AE=CF,由此可求出BE、AE的长.易证△AED∽△ADB,然后根据相似三角形的性质即可求出AD的长;
(4)在Rt△ADB中运用勾股定理可求出DB,结合(1)中的结论AD2=DG•DB可求出DG的长,然后在Rt△ADG中运用勾股定理即可求出AG的长.
(2)易证△DAG∽△DBA,根据相似三角形的性质可得AD2=DG•DB,由AD=ID即可得到ID2=DG•DB;
(3)过点D作DE⊥AB于E,过点D作DF⊥BC于F,连接DC,如图2.根据勾股定理可得AB=5,易证△BED≌△BFD,则有DE=DF,BE=BF.由∠ABD=∠CBD可得DA=DC,然后根据勾股定理证到AE=CF,由此可求出BE、AE的长.易证△AED∽△ADB,然后根据相似三角形的性质即可求出AD的长;
(4)在Rt△ADB中运用勾股定理可求出DB,结合(1)中的结论AD2=DG•DB可求出DG的长,然后在Rt△ADG中运用勾股定理即可求出AG的长.
解答:解:(1)连接AI,如图1,
∵点I是△ABC的内心,
∴∠BAI=∠CAI,∠ABI=∠CBI,
∵∠DAC=∠DBC,∴∠ABI=∠DAC,
∴∠DAI=∠DAC+∠IAC=∠ABI+∠BAI=∠AID,
∴AD=DI;
(2)ID2=DG•DB.
证明:∵∠ABD=∠DAG,∠D=∠D,
∴△DAG∽△DBA,
∴
=
,
∴AD2=DG•DB.
∵AD=ID,
∴ID2=DG•DB;
(3)过点D作DE⊥AB于E,过点D作DF⊥BC于F,连接DC,如图2.
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°.
∵AC=4,BC=3,
∴AB=5.
在△BED和△BFD中,
,
∴△BED≌△BFD(AAS),
∴DE=DF,BE=BF.
∵∠ABD=∠CBD,
∴DA=DC,
∴AE2=AD2-DE2=DC2-DF2=CF2,
∴AE=CF,
∴AB-BE=BF-BC,
∴5-BE=BE-3,
∴BE=4,
∴AE=AB-BE=5-4=1.
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△AED∽△ADB,
∴
=
,
∴AD2=AE•AB=1×5=5,
∴AD=
,
即AD的长为
;
(4)在Rt△ADB中,
DB=
=
=2
.
由(1)得AD2=DG•DB,
∴DG=
=
.
在Rt△ADG中,
AG=
=
=
,
∴在(3)的条件下,DG的长为
,AG的长为
.

∵点I是△ABC的内心,
∴∠BAI=∠CAI,∠ABI=∠CBI,
∵∠DAC=∠DBC,∴∠ABI=∠DAC,
∴∠DAI=∠DAC+∠IAC=∠ABI+∠BAI=∠AID,
∴AD=DI;
(2)ID2=DG•DB.
证明:∵∠ABD=∠DAG,∠D=∠D,
∴△DAG∽△DBA,
∴
| AD |
| BD |
| GD |
| AD |
∴AD2=DG•DB.
∵AD=ID,
∴ID2=DG•DB;
(3)过点D作DE⊥AB于E,过点D作DF⊥BC于F,连接DC,如图2.
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°.
∵AC=4,BC=3,
∴AB=5.
在△BED和△BFD中,

|
∴△BED≌△BFD(AAS),
∴DE=DF,BE=BF.
∵∠ABD=∠CBD,
∴DA=DC,
∴AE2=AD2-DE2=DC2-DF2=CF2,
∴AE=CF,
∴AB-BE=BF-BC,
∴5-BE=BE-3,
∴BE=4,
∴AE=AB-BE=5-4=1.
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△AED∽△ADB,
∴
| AD |
| AB |
| AE |
| AD |
∴AD2=AE•AB=1×5=5,
∴AD=
| 5 |
即AD的长为
| 5 |
(4)在Rt△ADB中,
DB=
| AB2-AD2 |
| 25-5 |
| 5 |
由(1)得AD2=DG•DB,
∴DG=
| 5 | ||
2
|
| ||
| 2 |
在Rt△ADG中,
AG=
| AD2+DG2 |
5+
|
| 5 |
| 2 |
∴在(3)的条件下,DG的长为
| ||
| 2 |
| 5 |
| 2 |
点评:本题主要考查了圆周角与弦的关系、圆周角定理、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识,综合性比较强,利用(1)中的结论将ID转化为AD是解决第(2)小题的关键,过∠ABC的角平分线上点D向两边作垂线段构造全等三角形是解决第(3)小题的关键,运用相似三角形的性质是解决第(4)小题的关键.

练习册系列答案
相关题目
下列从左到右的变形中是因式分解的有( )
①x2-y2-1=(x+y)(x-y)-1
②x4m+xm=xm(x3m+1)
③(x-y)2=x2-2xy+y2
④x2-9y2=(x+3y)(x-3y)
①x2-y2-1=(x+y)(x-y)-1
②x4m+xm=xm(x3m+1)
③(x-y)2=x2-2xy+y2
④x2-9y2=(x+3y)(x-3y)
| A、1个 | B、2个 | C、3个 | D、4个 |
下列关于x的方程:①ax2+bx+c=0;②a2x+
=5;③3x2-x+5=0;④5x2-7+2x3=0.其中一元二次方程有( )
| 3 |
| a |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列四个数中,最小的数是( )
| A、|-6| | ||
| B、-2 | ||
| C、0 | ||
D、-
|
 如图,OP是∠AOB内任意一条射线,OM平分∠AOP,ON平分∠POB,∠MON=60°,求∠AOB的度数.
如图,OP是∠AOB内任意一条射线,OM平分∠AOP,ON平分∠POB,∠MON=60°,求∠AOB的度数.
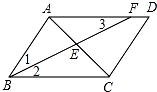 如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.
如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.