题目内容
6．
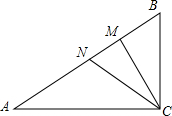如图，已知在Rt△ABC中，∠ACB=90°，AC=8，BC=6，AM=AC，BN=BC，求MN的长．
分析 根据勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方，即可得到AB长；再根据线段的相等关系可得到AM=8，BN=6，再根据线段的和差关系可以得到答案．
解答 解：∵∠ACB=90°，
∴AB2=AC2+CB2，
∵AC=8，BC=6，
∴AB=10；
∵AM=AC，BN=BC，
∴AM=8，BN=6，
∴AM+BN=AB+MN=14，
∴MN=14-10=4．
点评 此题主要考查了勾股定理以及线段的和差关系，关键是理清线段之间的关系．
练习册系列答案
相关题目
如图所示，张三打算在院落种上蔬菜．已知院落为东西长为32米，南北宽为20米的长方形，为了行走方便，要修筑同样宽度的三条小路，东西两条，南北一条，余下的部分种上各类蔬菜．若每条小路的宽均为1米．
11．对于任意实数h（h是常数），下列关于抛物线y=（x-h）2与抛物线y=x2+h的说法错误的是（ ）
| A． | 开口方向相同 | B． | 对称轴相同 | C． | 形状相同 | D． | 都有最低点 |
如图，已知AC=BC，CE=CD．试证明：∠EBA=∠DAB．
（1）作出如图三角形AB边上的高CD．