题目内容
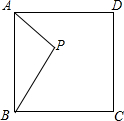 P为正方形ABCD内一点,且AP=2,将△APB绕点A按逆时针方向旋转90°得到△AP′D.
P为正方形ABCD内一点,且AP=2,将△APB绕点A按逆时针方向旋转90°得到△AP′D.(1)作出旋转后的图形;
(2)试求△APP′的周长和面积.
考点:作图-旋转变换,三角形的面积
专题:
分析:(1)利用题意得出对应点P′的位置进而得出答案;
(2)利用等腰直角三角形的性质求出周长和面积即可.
(2)利用等腰直角三角形的性质求出周长和面积即可.
解答: 解:(1)如图所示:△AP′D即为所求;
解:(1)如图所示:△AP′D即为所求;
(2)∵AP=2,将△APB绕点A按逆时针方向旋转90°得到△AP′D,
∴AP′=AP=2,∠PAP′=90°,
∴PP′=2
,
故△APP′的周长为:2+2+2
=4+2
;
△APP′的面积为:
×2×2=2.
 解:(1)如图所示:△AP′D即为所求;
解:(1)如图所示:△AP′D即为所求;(2)∵AP=2,将△APB绕点A按逆时针方向旋转90°得到△AP′D,
∴AP′=AP=2,∠PAP′=90°,
∴PP′=2
| 2 |
故△APP′的周长为:2+2+2
| 2 |
| 2 |
△APP′的面积为:
| 1 |
| 2 |
点评:此题主要考查了旋转的性质以及三角形面积求法,得出对应点位置是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,∠1=∠2,∠C=∠D,求证:AC=AD.
如图,∠1=∠2,∠C=∠D,求证:AC=AD.
 如图,已知在△ADC中,∠C=90°,AB⊥AC,D、E、B在一直线上,BE=2AD,求证:∠ADE=2∠EDC.
如图,已知在△ADC中,∠C=90°,AB⊥AC,D、E、B在一直线上,BE=2AD,求证:∠ADE=2∠EDC. 如图,正方形的棱长为3厘米,把所有的面分成3×3个小正方形,起边长都为1厘米,若一只蚂每秒爬行2.5厘米,则它下底面A点沿表面爬行至右侧面B点,最少要花
如图,正方形的棱长为3厘米,把所有的面分成3×3个小正方形,起边长都为1厘米,若一只蚂每秒爬行2.5厘米,则它下底面A点沿表面爬行至右侧面B点,最少要花