题目内容
16.已知二次函数y=ax2+bx+c(a<b)的图象恒不在x轴下方,且m<$\frac{a+b+c}{b-a}$恒成立.求m的取值范围.分析 利用二次函数的性质可判断a>0,b>0,c>0,b2-4ac≤0,则c≥$\frac{{b}^{2}}{4a}$,所以$\frac{a+b+c}{b-a}$≥$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$=$\frac{(2a+b)^{2}}{4a(b-a)}$,设b=a+m(m>0),于是$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$可表示为$\frac{(3a+m)^{2}}{4am}$,再利用(3a+m)2≥4•3a•m(当且仅当m=3a时取等号)可得$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$≥$\frac{4•3a•m}{4am}$,即$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$≥3,于是得到m<3.
解答 解:根据题意得a>0,b>0,c>0,b2-4ac≤0,则c≥$\frac{{b}^{2}}{4a}$,
所以$\frac{a+b+c}{b-a}$≥$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$,
而$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$=$\frac{4{a}^{2}+4ab+{b}^{2}}{4a(b-a)}$=$\frac{(2a+b)^{2}}{4a(b-a)}$,
由题设得b>a>0,设b=a+m(m>0),
则$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$=$\frac{(3a+m)^{2}}{4am}$,
因为a>0,m>0,则(3a+m)2≥4•3a•m(当且仅当m=3a时取等号),
则$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$=$\frac{(3a+m)^{2}}{4am}$≥$\frac{4•3a•m}{4am}$,即$\frac{a+b+\frac{{b}^{2}}{4a}}{b-a}$≥3,
而m<$\frac{a+b+c}{b-a}$,
所以m<3.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程;对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数.也考查了二次函数的性质.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案| A. | m≠3 | B. | m≠0或m≠3 | C. | m≠0 | D. | m≠0且m≠3 |
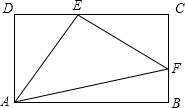 如图,四边形ABCD为矩形,E为CD上一点(不与C、D重合),F为BC上一点(不与C、B重合),△AEF的面积能否达到矩形ABCD面积的一半?请说明理由.
如图,四边形ABCD为矩形,E为CD上一点(不与C、D重合),F为BC上一点(不与C、B重合),△AEF的面积能否达到矩形ABCD面积的一半?请说明理由.



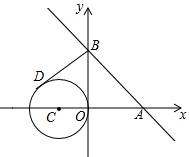 如图,直线y=-x+2与x轴、y轴分别交于点A,B,C(-1,0),且圆C的半径为1.若BD切圆C于点D,点D在第二象限,求点D的坐标.
如图,直线y=-x+2与x轴、y轴分别交于点A,B,C(-1,0),且圆C的半径为1.若BD切圆C于点D,点D在第二象限,求点D的坐标.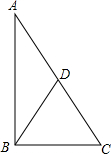 如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.
如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.
 如图:
如图: