题目内容
8.在△ABC中,∠B=30°,AB=2AC,求证:△ABC为直角三角形.分析 作AD⊥BC于D,根据直角三角形的性质得到AB=2AD,根据题意得到点D与点C重合,证明结论.
解答 证明: 作AD⊥BC于D,
作AD⊥BC于D,
在Rt△BAD中,∠B=30°,
∴AB=2AD,又AB=2AC,
∴点D与点C重合,
∴△ABC为直角三角形.
点评 本题考查的是直角三角形的性质,掌握30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,有一只蚂蚁从一个圆柱体的A点沿着侧面绕圆柱至少一圈爬到B点,已知圆柱的底面半径为1.5cm,高为12cm,则蚂蚁所走过的最短路径是多少?(π取3)
如图,有一只蚂蚁从一个圆柱体的A点沿着侧面绕圆柱至少一圈爬到B点,已知圆柱的底面半径为1.5cm,高为12cm,则蚂蚁所走过的最短路径是多少?(π取3)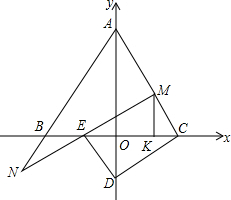 已知B(-2,0),C(2,0),点A是y轴正半轴上一点,CD⊥AC交y轴于D,M为AC上一动点.N为AB延长线一动点,且满足AM+AN=2AC,MN交BC于E,连DE.
已知B(-2,0),C(2,0),点A是y轴正半轴上一点,CD⊥AC交y轴于D,M为AC上一动点.N为AB延长线一动点,且满足AM+AN=2AC,MN交BC于E,连DE. 如图,将纸片△ABC沿DE折叠,点A落在点F处.
如图,将纸片△ABC沿DE折叠,点A落在点F处. 如图所示,在?ABCD中,∠BAD的平分线与∠ABC的平分线、∠ADC的平分线分别交于点E和点F,∠BCD的平分线与∠ABC的平分线、∠ADC的平分线分别交于点H和点G.
如图所示,在?ABCD中,∠BAD的平分线与∠ABC的平分线、∠ADC的平分线分别交于点E和点F,∠BCD的平分线与∠ABC的平分线、∠ADC的平分线分别交于点H和点G. 在△ABC中,AD是∠BAC的角平分线,EF⊥BC,∠B>∠C,证明:∠FED=$\frac{1}{2}$(∠B-∠C)
在△ABC中,AD是∠BAC的角平分线,EF⊥BC,∠B>∠C,证明:∠FED=$\frac{1}{2}$(∠B-∠C)