题目内容
5. 如图,直线y=kx+b与双曲线y=$\frac{4-2m}{x}$交于A,B两点,与x轴交于点P,过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D.
如图,直线y=kx+b与双曲线y=$\frac{4-2m}{x}$交于A,B两点,与x轴交于点P,过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D.(1)求m的取值范围;
(2)若点A的坐标为(-2,-4),$\frac{BP}{AP}$=$\frac{1}{4}$,求m的值和直线AB对应的函数表达式;
(3)连接CD,判断CD与AB的位置关系,并说明理由.
分析 (1)由图象可知,双曲线y=$\frac{4-2m}{x}$在一三象限,则4-2m>0,求得m<2;
(2)作BE⊥x轴于E,把A点的坐标代入,即可求得m的值,根据AC∥BE,则$\frac{BE}{AC}$=$\frac{BP}{AP}$=$\frac{1}{4}$,求得BE=$\frac{1}{4}$AC=1,代入解析式即可求得B的坐标,然后关键待定系数法即可求得直线的解析式;
(3)分别求得OC=2,AC=4,OD=1,OP=6,得出CP=2+6=8,然后证得△COD∽△PCA,证得∠DCO=∠CPA,即可证得CD∥AB.
解答  解:(1)由图象可知,双曲线y=$\frac{4-2m}{x}$在一三象限,
解:(1)由图象可知,双曲线y=$\frac{4-2m}{x}$在一三象限,
∴4-2m>0,
解得m<2;
(2)作BE⊥x轴于E,
∵AC⊥x轴,
∴AC∥BE,
∴$\frac{BE}{AC}$=$\frac{BP}{AP}$=$\frac{1}{4}$,
∴BE=$\frac{1}{4}$AC,
∵点A的坐标为(-2,-4),
∴4-2m=-2×(-4)=8,
解得m=-2,
∵AC=4,
∴BE=1,
∴B(8,1),
把A、B点的坐标代入y=kx+b得$\left\{\begin{array}{l}{8k+b=1}\\{-2k+b=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-3}\end{array}\right.$,
∴直线AB对应的函数表达式为y=$\frac{1}{2}$x-3;
(3)∵A(-2,-4),B(8,1),
∴OC=2,AC=4,OD=1,
由直线y=$\frac{1}{2}$x-3可知P(6,0),
∴CP=2+6=8,
∴$\frac{OC}{OD}$=$\frac{CP}{AC}$=$\frac{2}{1}$,
∵∠COD=∠AOP=90°,
∴△COD∽△PCA,
∴∠DCO=∠CPA,
∴CD∥AB.
点评 本题考查了反比例函数和一次函数的交点问题,待定系数法求一次函数的解析式,三角形相似的判断和性质,平行线的判定等,根据三角形相似求得B点的坐标是解题的关键.

 如图,AB是圆O的直径,C,D分别为圆周上直径AB两侧的点,若∠ADC=3∠CAB.求∠CAB的度数.
如图,AB是圆O的直径,C,D分别为圆周上直径AB两侧的点,若∠ADC=3∠CAB.求∠CAB的度数. 为了改善市民的生活环境,某市在江滨空地修建一个如图所示的休闲文化广场,△ABC是直角三角形,∠ACB=90°;又分别以AB,BC,AC为直径作半圆,它们交出两弯新月形状(图中阴影部分),两弯新月部分栽植花草,其余空地铺设地砖,设AC=b,BC=a,AB=c,求:
为了改善市民的生活环境,某市在江滨空地修建一个如图所示的休闲文化广场,△ABC是直角三角形,∠ACB=90°;又分别以AB,BC,AC为直径作半圆,它们交出两弯新月形状(图中阴影部分),两弯新月部分栽植花草,其余空地铺设地砖,设AC=b,BC=a,AB=c,求: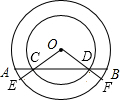 如图,以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D,OC、OD的延长线交大圆于E、F.求证:$\widehat{AE}$=$\widehat{BF}$.
如图,以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D,OC、OD的延长线交大圆于E、F.求证:$\widehat{AE}$=$\widehat{BF}$.