题目内容
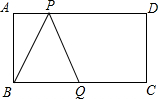如图：长方形ABCD中，AD=10，AB=4，点Q是BC的中点，点P在AD边上运动，当△BPQ是等腰三角形时，AP的长为考点：等腰三角形的判定,矩形的性质
专题：动点型
分析：分BP=PQ、BP=BQ和BQ=PQ三种情况分别讨论，再结合勾股定理求解即可．
解答：解：∵四边形ABCD为矩形，且AD=10，
∴BQ=5，
当BP=PQ时，过P作PM⊥BQ，交BQ于点M，如图1，
则BM=MQ=2.5，且四边形ABMP为矩形，
∴AP=BM=2.5，
当BQ=BP时，则BP=5，在Rt△ABP中，AB=4，由勾股定理可求得AP=3，
当PQ=BQ时，以点Q为圆心，BQ为半径作圆，于AD交于R、S两点，如图2，
过Q作QN⊥RS，交RS于点N，则可知RN=SN，
在Rt△RNQ中，可求得RN=SN=3，
则AR=2，AS=8，
即R、S为满足条件的P点的位置，
∴AP=2或8，
综上可知AP为2或2.5或3或8，
故答案为：2或2.5或3或8．
∴BQ=5，
当BP=PQ时，过P作PM⊥BQ，交BQ于点M，如图1，
则BM=MQ=2.5，且四边形ABMP为矩形，
∴AP=BM=2.5，
当BQ=BP时，则BP=5，在Rt△ABP中，AB=4，由勾股定理可求得AP=3，
当PQ=BQ时，以点Q为圆心，BQ为半径作圆，于AD交于R、S两点，如图2，
过Q作QN⊥RS，交RS于点N，则可知RN=SN，
在Rt△RNQ中，可求得RN=SN=3，
则AR=2，AS=8，
即R、S为满足条件的P点的位置，
∴AP=2或8，
综上可知AP为2或2.5或3或8，
故答案为：2或2.5或3或8．
点评：本题主要考查等腰三角形的性质，分三种情况讨论是解题的关键．注意利用画圆可以找到满足条件的点．
练习册系列答案
相关题目
AD是△ABC的角平分线，作DE⊥AB于E，DF⊥AC于F，下列结论错误的是（ ）
| A、DE=DF |
| B、AE=AF |
| C、BD=CD |
| D、∠ADE=∠ADF |
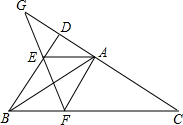在△ABC中，以边AB为轴翻折∠ABC，使翻折后BC的对应边交CA的延长线于点D．分别过A作AE∥BC交BD于E，作AF∥BD交BC于F，延长CD、EF交于G．若BC=2BD，BE=1，求DE的长
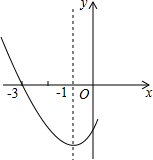如图是二次函数y=ax2+bx+c图象的一部分，其对称轴是x=-1，且过点（-3，0），下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0；④若（-5，y1），（