题目内容
3.一个口袋中装有3个白球、5个红球,这些球除了颜色外完全相同,充分摇匀后随机摸出一球,发现是白球(1)如果将这个白球放回,再摸出一球,它是白球的概率是多少?
(2)如果将这个白球不放回,再摸出一球,它是白球的概率是多少?
分析 (1)摸出一个白球放回对第二次摸到白球没有影响,直接利用概率公式求解即可;
(2)如果这个白球不放回,则总数减少1,再利用概率公式求解即可.
解答 解:
(1)∵${P_{(白球)}}=\frac{3}{5+3}=\frac{3}{8}$,
∴它是白球的概率是$\frac{3}{8}$.
(2)∵${P_{(白球)}}=\frac{3-1}{5+3-1}=\frac{2}{7}$
∴它是白球的概率是$\frac{2}{7}$.
点评 本题考查了概率的公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.计算正确的是( )
| A. | 3.4×104=340000 | B. | m×2m2=3m2 | C. | (-$\frac{1}{2}$mn2)2=m2n4 | D. | 4xy-4yx=0 |
 如图,?ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.
如图,?ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.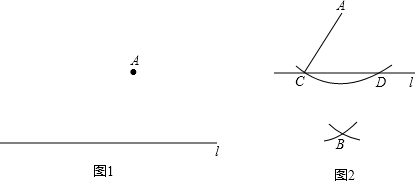
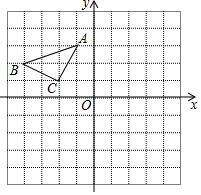 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.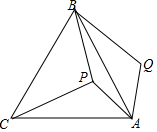 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.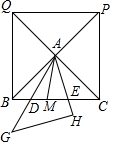 如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.
如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.