题目内容
关于x的一元二次方程ax2+bx+c=0，如果a＜0，a+c＞-b，那么ax2+bx+c=-2的根的情况是（ ）
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、必有一个根为0 |
考点：根的判别式
专题：
分析：根据一元二次方程和二次函数的关系解答．
解答：
解：对于y=ax2+bx+c，
a＜0则开口向下，
a+c＞-b，即a+b+c＞0，可知当x=1时y＞0，即y1＞0，
如图：ax2+bx+c=-2时，即y=-2时，有两个不相等的实数根x1，x2．
故选A．
解：对于y=ax2+bx+c，a＜0则开口向下，
a+c＞-b，即a+b+c＞0，可知当x=1时y＞0，即y1＞0，
如图：ax2+bx+c=-2时，即y=-2时，有两个不相等的实数根x1，x2．
故选A．
点评：本题考查了一元二次方程和二次函数的关系，根据题意画出图形即可直观的出结论．
练习册系列答案
53随堂测系列答案
相关题目
下列结论正确的是（ ）
| A、近似数5.210和5.21表示的意义相同 |
| B、近似数76.0是精确到个位的数 |
| C、6.350×104是精确到十位的近似数 |
| D、近似数7千与近似数7000的精确度相同 |
一农民带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，他手中持有的钱数（含备用零钱）y与售出的土豆千克数x的关系如图所示，结合图象回答下列问题．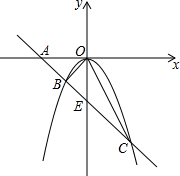
已知直线AB过x轴上一点A（-2，0），且与抛物线y=ax2交于B、C两点，C（2，-4）．
如图，直线AB，CD，EF相交于点O，且∠AOE=15°，∠BOC=2∠AOC，求∠DOF的度数．