题目内容
3.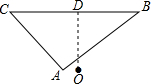 如图,△ABC中,∠A=90°,OD⊥BC,OD=DC=DB,请以O为中心将△ABC顺时针旋转90°,180°,270°,画出这个图案.
如图,△ABC中,∠A=90°,OD⊥BC,OD=DC=DB,请以O为中心将△ABC顺时针旋转90°,180°,270°,画出这个图案.(1)请问前后图案的边界组成了什么图形?
(2)能用这个图案验证勾股定理吗?
分析 (1)根据旋转图形的特征,这个图形绕O点顺时针旋转90°,180°,270°后,O点的位置不动,其余各部分均绕O点按相同的方向旋转相同的角度.
(2)采用面积法证明.
解答 解:(1)如图所示:前后4个图形的边界组成了正方形.
(2)可以证明勾股定理.证明:如图所示两直角边及斜边长分别为a、b、c.则有正方形面积:S=c•c=c2,
又有:S=4×$\frac{1}{2}$ab+(b-a)2=2ab+b2-2ab+a2=a2+b2,
故:a2+b2=c2所以即可得证勾股定理.
点评 考查勾股定理的证明.注意:图形旋转四要素分别是原位置、旋转中心、旋转方向、旋转角.

练习册系列答案
相关题目
10.某大型超市买进了某种水果1000千克,进价为7元/千克,销售价定为11元/千克,销售一半后为了尽快卖完,准备打折出售.如果要使总利润不低于2900元,那么余下的水果至多可按原销售定价的几折出售?
13. 如图,四边形ABCD内接于⊙O,若四边形ABCD的外角∠DCE=70°,则∠BAD的度数为( )
如图,四边形ABCD内接于⊙O,若四边形ABCD的外角∠DCE=70°,则∠BAD的度数为( )
 如图,四边形ABCD内接于⊙O,若四边形ABCD的外角∠DCE=70°,则∠BAD的度数为( )
如图,四边形ABCD内接于⊙O,若四边形ABCD的外角∠DCE=70°,则∠BAD的度数为( )| A. | 140° | B. | 110° | C. | 220° | D. | 70° |
 如图,点D在△ABC的AB边上.
如图,点D在△ABC的AB边上.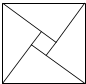 四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.
四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.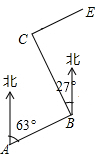 柳林乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东63°方向到B村,从B村沿北偏西27°方向到C村,水渠从C村沿北偏东63°方向修建,可以保持AB的方向一致.
柳林乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东63°方向到B村,从B村沿北偏西27°方向到C村,水渠从C村沿北偏东63°方向修建,可以保持AB的方向一致.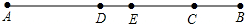 如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.
如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.