Question

9．已知抛物线y=a（x-h）²的对称轴是直线x=-1，与y轴交于（0，2）．
（1）求抛物线的解析式；
（2）画出它的图象；
（3）当x为何值时，y随x增大而减小？

Answer 1

分析 （1）根据对称轴，可得h的值，根据抛物线与y轴的交点，可得a值，从而求得抛物线的解析式；
（2）根据解析式画出图象即可；
（3）根据图象即可求得．

解答 解：（1）已知抛物线y=a（x-h）²的对称轴为直线x=-1，
h=-1，抛物线y=a（x+1）²与y轴交于点（0，2），
把（0，2）代入y=a（x+1）²得
a=2，
解得a=2．
∴抛物线的解析式为y=2（x+1）²．
（2）画出函数图象如图：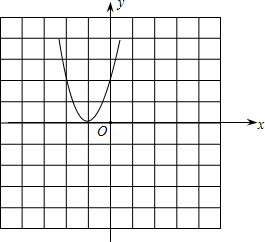

（3）由图象可知：当x＞-1时，y随x增大而减小．

点评 本题考查了待定系数法求函数解析式以及二次函数的性质，掌握顶点式是解决问题的关键．