题目内容
3.在Rt△ABC中,∠C=90°,∠A,∠B的对边分别是a,b.(1)取a=5,b=12,求∠A,∠B的正切值;
(2)再取两组不同的a,b的值,求∠A,∠B的正切值;
(3)观察(1),(2)中的计算结果,你发现了什么?
分析 (1)根据正切函数的定义,得tanA=$\frac{a}{b}$,tanB=$\frac{b}{a}$,将a=5,b=12分别代入,即可求出∠A,∠B的正切值;
(2)取两组不同的a,b的值,分别代入tanA=$\frac{a}{b}$,tanB=$\frac{b}{a}$,即可求出∠A,∠B的正切值;
(3)观察(1),(2)中的计算结果,可以发现tanA•tanB=1.
解答 解:在Rt△ABC中,∠C=90°,∠A,∠B的对边分别是a,b.
(1)∵a=5,b=12,
∴tanA=$\frac{a}{b}$=$\frac{5}{12}$,tanB=$\frac{b}{a}$=$\frac{12}{5}$;
(2)取a=3,b=4,则tanA=$\frac{a}{b}$=$\frac{3}{4}$,tanB=$\frac{b}{a}$=$\frac{4}{3}$;
再取a=9,b=40,则tanA=$\frac{a}{b}$=$\frac{9}{40}$,tanB=$\frac{b}{a}$=$\frac{40}{9}$;
(3)观察(1),(2)中的计算结果,可以发现:
如果∠A+∠B=90°,那么tanA•tanB=1.
点评 本题考查了将直角三角形,掌握正切函数的定义:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA是解题的关键.

练习册系列答案
相关题目
11.关于x的方程a-3(x+5)=b(x+2)是一元一次方程,则( )
| A. | b=2 | B. | b=-3 | C. | b≠2 | D. | b≠-3 |
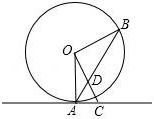 如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥0B,连结AB交OC于点D.
如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥0B,连结AB交OC于点D.