题目内容
13.阅读填空:对于方程组$\left\{\begin{array}{l}{4(x+y)-3(x-y)=14}\\{\frac{x+y}{2}+\frac{x-y}{3}=6}\end{array}\right.$,不妨设$\frac{x+y}{2}=u,\frac{x-y}{3}=v$,则原方程组变为以u,v为未知数的方程组$\left\{\begin{array}{l}{8u-9v=14}\\{u+v=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{u=4}\\{v=2}\end{array}\right.$,从而原方程组的解是$\left\{\begin{array}{l}{x=7}\\{y=1}\end{array}\right.$,这种解法称之为“换元法”分析 根据设出的u与v,将方程组变形,求出解确定出u与v的值,进而求出x与y的值.
解答 解:阅读填空:对于方程组$\left\{\begin{array}{l}{4(x+y)-3(x-y)=14}\\{\frac{x+y}{2}+\frac{x-y}{3}=6}\end{array}\right.$,
不妨设$\frac{x+y}{2}$=u,$\frac{x-y}{3}$=v,则原方程组变为以u,v为未知数的方程组$\left\{\begin{array}{l}{8u-9v=14}\\{u+v=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{u=4}\\{v=2}\end{array}\right.$,从而原方程组的解是$\left\{\begin{array}{l}{x=7}\\{y=1}\end{array}\right.$,这种解法称之为“换元法”.
故答案为:$\left\{\begin{array}{l}{8u-9v=14}\\{u+v=6}\end{array}\right.$;$\left\{\begin{array}{l}{u=4}\\{v=2}\end{array}\right.$;$\left\{\begin{array}{l}{x=7}\\{y=1}\end{array}\right.$
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.下列函数中,y的值随x值的增大而减小的是( )
①y=8x-1;②y=-0.6x;③y=$\sqrt{5}$x+1;④y=($\sqrt{2}$-$\frac{3}{2}$)x.
①y=8x-1;②y=-0.6x;③y=$\sqrt{5}$x+1;④y=($\sqrt{2}$-$\frac{3}{2}$)x.
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
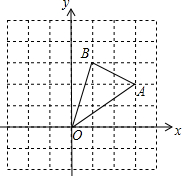 如图,在边长为1的正方形组成网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3),将△AOB绕点O逆时针旋转90°
如图,在边长为1的正方形组成网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3),将△AOB绕点O逆时针旋转90°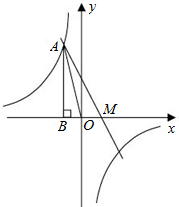 如图,已知反比例函数$y=\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数$y=\frac{k}{x}$的图象上另一点C(n,-2).
如图,已知反比例函数$y=\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数$y=\frac{k}{x}$的图象上另一点C(n,-2).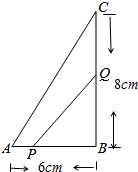 如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动.
如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动.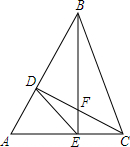 如图,△ABC中,∠A=60°,△ABC高BE、CD交于点F,下列说法中:①AD•AB=AE•AC,②BF•EF=CF•DF,③S△ABC=4S△AED,④BC=2DE,其中正确的有( )
如图,△ABC中,∠A=60°,△ABC高BE、CD交于点F,下列说法中:①AD•AB=AE•AC,②BF•EF=CF•DF,③S△ABC=4S△AED,④BC=2DE,其中正确的有( )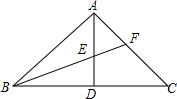 如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.
如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.