题目内容
12.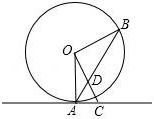 如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥0B,连结AB交OC于点D.
如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥0B,连结AB交OC于点D.(1)求证:AC=CD;
(2)若AC=2,AO=$\sqrt{5}$,求BD的长度.
分析 (1)根据切线的性质可得出,∠OAC=90°,再由已知条件得∠ODB+∠B=90°,由OA=OB可得出∠OAB=∠B,从而得出∠CAB=∠ADC,即AC=CD.
(2)利用勾股定理求出OC,即可得出OD的长,然后再根据勾股定理即可得到结论.
解答 (1)证明:∵AC是⊙切线,
∴OA⊥AC,
∴∠OAC=90°,
∴∠OAB+∠CAB=90°.
∵OC⊥OB,
∴∠COB=90°,
∴∠ODB+∠B=90°.
∵OA=OB
∴∠OAB=∠B,
∴∠CAB=∠ODB.
∵∠ODB=∠ADC,
∴∠CAB=∠ADC
∴AC=CD;
(2)解:在Rt△OAC中,OC=$\sqrt{O{A}^{2}+A{C}^{2}}$=3,
∴OD=OC-CD=OC-AC=3-2=1,
∵OB=OA=$\sqrt{5}$,
∴BD=$\sqrt{O{D}^{2}+O{B}^{2}}$=$\sqrt{6}$.
点评 本题考查了切线的性质,勾股定理,等腰三角形的判定和性质,证明线段的相等一般证明这个三角形的两个角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.计算(-$\frac{1}{2}$x2y)3+($\frac{1}{4}$x2y)2•(-x2y)的结果为( )
| A. | -$\frac{3}{16}$x6y3 | B. | 0 | C. | -x6y3 | D. | -$\frac{5}{12}$x6y3 |
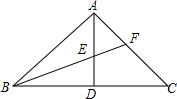 如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.
如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.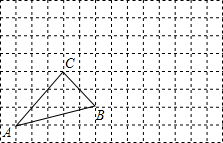 如图.把△ABC向右平移5个方格,再绕点B顺时针方向旋转90°.
如图.把△ABC向右平移5个方格,再绕点B顺时针方向旋转90°.