题目内容
20.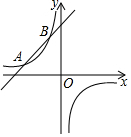 如图,一次函数的图象与反比例函数的图象交于A(-3,1)、B(m,3)两点,
如图,一次函数的图象与反比例函数的图象交于A(-3,1)、B(m,3)两点,(1)求反比例函数和一次函数的解析式;
(2)写出使一次函数的值大于反比例函数的x的取值范围;
(3)连接AO、BO,求△ABO的面积.
分析 (1)设一次函数的解析式为y=kx+b(k≠0),反比例函数的解析式为y=$\frac{a}{x}$(a≠0),把A(-3,1)代入y=$\frac{a}{x}$即可求出反比例函数的解析式,把B(m,3)代入y=-$\frac{3}{x}$求出B的坐标,把A、B的坐标代入y=kx+b求出k、b,即可求出一次函数的解析式;
(2)根据A、B的坐标和图象得出即可;
(3)求出一次函数和两坐标轴的交点坐标,再根据三角形的面积公式求出即可.
解答 解:(1)设一次函数的解析式为y=kx+b(k≠0),反比例函数的解析式为y=$\frac{a}{x}$(a≠0),
把A(-3,1)代入y=$\frac{a}{x}$得:a=-3,
即反比例函数的解析式为y=-$\frac{3}{x}$,
把B(m,3)代入y=-$\frac{3}{x}$得:3=-$\frac{3}{m}$,
解得:m=-1,
即B的坐标为(-1,3),
把A、B的坐标代入y=kx+b得:$\left\{\begin{array}{l}{-3k+b=1}\\{-k+b=3}\end{array}\right.$,
解得:k=1,b=4,
即一次函数的解析式为y=x+4;
(2)∵函数y=-$\frac{3}{x}$和y=x+4的交点为A(-3,1)、B(-1,3),
∴使一次函数的值大于反比例函数的x的取值范围是-3<x<-1或x>0;
(3)
设一次函数y=x+4和x轴的交点为N,和y轴的交点为M,
当x=0时,y=4,当y=0时,x=-4,
即OM=4,ON=4,
∵A(-3,1)、B(-1,3),
∴△ABO的面积为S△MON-S△BOM-S△AON=$\frac{1}{2}$×4×4-$\frac{1}{2}$×4×1-$\frac{1}{2}$×4×1=4.
点评 本题考查了用待定系数法求一次函数和反比例函数的解析式,一次函数和反比例函数的交点问题等知识点,能够求出函数的解析式是解此题的关键.

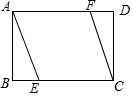 如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )
如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )| A. | $\sqrt{5}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{13}{6}$ |
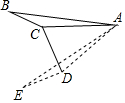 如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.
如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°. 如图,⊙O的直径AB=5,弦AC=3,△PEF的顶点在△ABC的边上,EF∥CB,PB=2EC,设EC=t,△PEF的面积为S.
如图,⊙O的直径AB=5,弦AC=3,△PEF的顶点在△ABC的边上,EF∥CB,PB=2EC,设EC=t,△PEF的面积为S.