题目内容
19.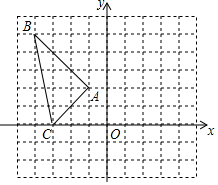 如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,
如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,(1)请画出平移后的图形△A′B′C′;
(2)并写出△A′B′C′各顶点的坐标;
(3)求出△A′B′C′的面积.
分析 (1)根据图形平移的性质画出△A′B′C′即可;
(2)根据各点在坐标系中的位置写出各点坐标即可;
(3)利用矩形的面积减去三个顶点上三角形的面积即可.
解答  解:(1)如图,△A′B′C′即为所求;
解:(1)如图,△A′B′C′即为所求;
(2)由图可知,A′(4,0),B′(1,3),C′(2,-2);
(3)S△A′B′C′=5×3-$\frac{1}{2}$×1×5-$\frac{1}{2}$×2×2-$\frac{1}{2}$×3×3=6.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
7.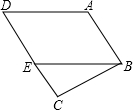 如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
解:∵AB∥CD (已知)
∴∠ABE=∠BEC(两直线平行,内错角相等)
∵AD∥BE (已知)
∴∠D=∠BCE
∴∠ABE=∠D ( 等量代换)
 如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.解:∵AB∥CD (已知)
∴∠ABE=∠BEC(两直线平行,内错角相等)
∵AD∥BE (已知)
∴∠D=∠BCE
∴∠ABE=∠D ( 等量代换)
14.若$\sqrt{x-1}$+(y+2)2=0,则(x+y)2017=( )
| A. | -1 | B. | 1 | C. | 32017 | D. | -32017 |
4. 如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
①左、右两个几何体的主视图相同
②左、右两个几何体的俯视图相同
③左、右两个几何体的左视图相同.
 如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )①左、右两个几何体的主视图相同
②左、右两个几何体的俯视图相同
③左、右两个几何体的左视图相同.
| A. | ①②③ | B. | ②③ | C. | ①② | D. | ①③ |
9.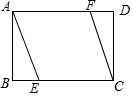 如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )
如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )
 如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )
如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )| A. | $\sqrt{5}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{13}{6}$ |
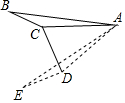 如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.
如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.