题目内容
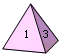如图，均匀的正四面体的各面依次标有1，2，3，4四个数字．小明做了60次投掷试验，结果统计如下：| 朝下数字 | 1 | 2 | 3 | 4 |
| 出现的次数 | 16 | 20 | 14 | 10 |
（2）随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．
考点：列表法与树状图法,利用频率估计概率
专题：
分析：（1）根据试验中“4朝下”的总次数除以总数即可得出答案；
（2）列表列举出所有的可能的结果，然后利用概率公式解答即可．
（2）列表列举出所有的可能的结果，然后利用概率公式解答即可．
解答：解：（1）“4朝下”的频率：
=
，
故答案为：
；
（2）随机投掷正四面体两次，所有可能出现的结果如下：
总共有16种结果，每种结果出现的可能性相同，而两次朝下数字之和大于4的结果有10种．
∴P（两次朝下的数字之和大于4）=
．
| 10 |
| 60 |
| 1 |
| 6 |
故答案为：
| 1 |
| 6 |
（2）随机投掷正四面体两次，所有可能出现的结果如下：
| 第一次 第二次 | 1 | 2 | 3 | 4 |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） |
∴P（两次朝下的数字之和大于4）=
| 10 |
| 16 |
| 5 |
| 8 |
点评：本题主要考查列表法与树状图法求概率，以及频率的意义，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，有一块边长为24m的正方形绿地，绿地周边是小路，在绿地旁边的B处有健身器材，BC=7m．请你算一算，如果居住在A处的居民为了走近路而不惜践踏草地直接从A到B，这样比沿着绿地周边的小路，仅少走多少米？
如图，射线OC在∠AOB的内部，射线OM是∠AOC的平分线，射线ON是∠BOC的平分线．
从一个直径为4