题目内容
因式分解：
（1）（a+1）（a-1）+a（a-1）；
（2）y3-2xy2+x2y．
（1）（a+1）（a-1）+a（a-1）；
（2）y3-2xy2+x2y．
考点：提公因式法与公式法的综合运用
专题：计算题
分析：（1）原式提取公因式即可得到结果；
（2）原式提取y，再利用完全平方公式分解即可．
（2）原式提取y，再利用完全平方公式分解即可．
解答：解：（1）原式=（a-1）（a+1+a）=（a-1）（2a+1）；
（2）原式=y（y2-2xy+x2）=y（x-y）2．
（2）原式=y（y2-2xy+x2）=y（x-y）2．
点评：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
下列一元二次方程中，有两个相等实数根的方程是（ ）
| A、x2+2=0 |
| B、x2+x+2=0 |
| C、x2+2x+1=0 |
| D、x2-x-2=0 |
反比例函数y=
（m≠3）在图象所在的每一象限内，函数值y随自变量x的增大而增大，则m的取值范围是（ ）
| m-3 |
| x |
| A、m＞3 | B、m＜3 |
| C、m＞-3 | D、m＜-3 |
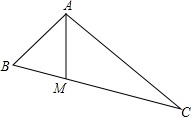如图，在Rt△ABC中，∠BAC=90°，AB=2，M为边BC上的点，连接AM．如果将△ABM沿直线AM翻折后，点B恰好落在边AC的中点处，那么点M到AC的距离是