题目内容
10.以AB为⊙O的直径,洋洋以点A为圆心,OA长为半径画弧,交⊙O于C,D两点,连接BC,BD,CD,根据洋洋的做法,可判断△BCD是等边三角形.分析 根据等半径圆,可得△AOC的形状,根据等边三角形的性质,可得CE、OE长,根据垂径定理,可得CD长,根据勾股定理,可得BC、BD长.
解答 解:如图: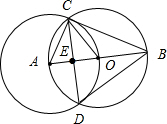 ⊙A、⊙O是半径相等的圆,
⊙A、⊙O是半径相等的圆,
△AOC是等边三角形,
CE=$\frac{\sqrt{3}}{2}$r,OE=$\frac{1}{2}$r,
CD=2OE=$\sqrt{3}$r.
BE=OE+OB=$\frac{3}{2}$r,
CB=$\sqrt{C{E}^{2}+B{E}^{2}}$=$\sqrt{(\frac{\sqrt{3}}{2}r)^{2}+(\frac{3}{2}r)^{2}}$=$\sqrt{3}$r,
同理BD=CB=CD=$\sqrt{3}$r.
△BCD是等边三角形,
故答案为:等边.
点评 本题考查了相交圆的性质,利用等半径圆得出△AOC的形状是解题关键,利用了垂径定理,勾股定理,等边三角形的判定.

练习册系列答案
相关题目
5.如果(2x+y-2)2+|3x-2y-10|=0,那么x和y的值为( )
| A. | x=2,y=2 | B. | x=-2,y=2 | C. | x=-2,y=-2 | D. | x=2,y=-2 |
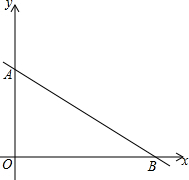 如图,一次函数y=-$\frac{3}{4}$x+6的图象分别与y轴、x轴交于点A、B,点P从点B出发,沿BA以每秒1个单位的速度向点A运动,当点P到达点A时停止运动,设点P的运动时间为t秒.
如图,一次函数y=-$\frac{3}{4}$x+6的图象分别与y轴、x轴交于点A、B,点P从点B出发,沿BA以每秒1个单位的速度向点A运动,当点P到达点A时停止运动,设点P的运动时间为t秒.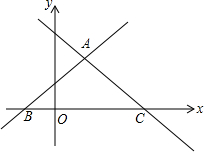 如图,在平面直角坐标系中,直线y=x+1与直线y=-$\frac{3}{4}$x+3,交于点A($\frac{8}{7}$,$\frac{15}{7}$),且两直线分别交x轴于B,C两点.
如图,在平面直角坐标系中,直线y=x+1与直线y=-$\frac{3}{4}$x+3,交于点A($\frac{8}{7}$,$\frac{15}{7}$),且两直线分别交x轴于B,C两点.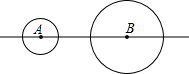 如图,⊙A、⊙B的半径分别为1cm、2cm,圆心距AB为5cm.将⊙A由图示位置沿直线AB向右平移,当该圆与⊙B内切时,⊙A平移的距离是4或6cm.
如图,⊙A、⊙B的半径分别为1cm、2cm,圆心距AB为5cm.将⊙A由图示位置沿直线AB向右平移,当该圆与⊙B内切时,⊙A平移的距离是4或6cm.