题目内容
6. 小明为一个矩形娱乐场所提供了如下的设计方案,其中半圆形休息区和矩形游泳池以外的地方都是绿地.
小明为一个矩形娱乐场所提供了如下的设计方案,其中半圆形休息区和矩形游泳池以外的地方都是绿地.(1)游泳池和休息区的面积各是多少?
(2)绿地的面积是多少?
(3)如果这个娱乐场所需要有一半以上的绿地,小明设计的m,n分别是a,b的$\frac{1}{2}$,当a=60米,b=40米时,他的设计方案符合要求吗?(π取值为3)
分析 (1)根据图形可以分别求得游泳池和休息区的面积;
(2)根据图形可以求得绿地的面积;
(3)根据题目中的数据可以求得小明设计的绿地的面积和娱乐场的面积,从而可以解答本题.
解答 解:(1)由题意可得,
游泳池的面积是:mn,
休息区的面积是:$π(\frac{n}{2})^{2}×\frac{1}{2}$=$\frac{π{n}^{2}}{8}$,
即游泳池的面积是mn,休息区的面积是$\frac{π{n}^{2}}{8}$;
(2)由图可知,
绿地的面积是:ab-mn-$\frac{π{n}^{2}}{8}$;
(3)∵m,n分别是a,b的$\frac{1}{2}$,
∴当a=60米,b=40米时,m=30米,n=20米,
∴此时绿地的面积是:60×40-30×20-$\frac{3×2{0}^{2}}{8}$=1650(平方米),
娱乐场的面积是:60×40=2400(平方米),
∵1650>$\frac{2400}{2}$=1200,
∴小明的设计方案符合要求.
点评 本题考查列代数式和代数式求值,解题的关键是明确题意,列出相应的代数式和求出相应的代数式的值.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是( )
| A. | [0)=0 | B. | 若[x)-x=0.5,则x=0.5 | ||
| C. | [x)-x的最小值是0 | D. | [x)-x的最大值是1 |
 如图:在平面直角坐标系中,直线y=x+3与x轴、y轴分别交于A,B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴于点E(1,0),点P(t,0)为x轴上一动点.若点T 为直线DE上一动点,当以O,B,T为顶点的三角形与以O,B,P为顶点的三角形相似时,则相应的点T(t<0)的坐标为(1,3)或(1,0)或(1,$\frac{3-\sqrt{5}}{2}$).
如图:在平面直角坐标系中,直线y=x+3与x轴、y轴分别交于A,B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴于点E(1,0),点P(t,0)为x轴上一动点.若点T 为直线DE上一动点,当以O,B,T为顶点的三角形与以O,B,P为顶点的三角形相似时,则相应的点T(t<0)的坐标为(1,3)或(1,0)或(1,$\frac{3-\sqrt{5}}{2}$).
 设计一个如图所示的槽缸,截面ABCD为矩形,AB+BC+CD=80cm
设计一个如图所示的槽缸,截面ABCD为矩形,AB+BC+CD=80cm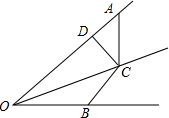 如图,OC平分∠AOB,AC=BC,CD⊥OA于D.
如图,OC平分∠AOB,AC=BC,CD⊥OA于D.