题目内容
14.在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.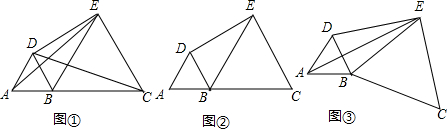
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2,试求∠DEB的度数.
分析 (1)欲证明CD=AE,只要证明△ABE≌△DBC即可.
(2)如图②中,取BE中点F,连接DF,首先证明△BDE是直角三角形,再利用勾股定理即可.
(3)如图③中,连接DC,先利用勾股定理的逆定理证明△DEC是直角三角形,得∠DEC=90°即可解决问题.
解答 (1)证明:如图①中,∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,
$\left\{\begin{array}{l}{AB=BD}\\{∠ABE=∠DBC}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△DBC,
∴AE=DC.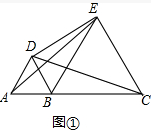
(2)解:如图②中,取BE中点F,连接DF.
∵BD=AB=1,BE=BC=2,∠ABD=∠EBC=60°,
∴BF=EF=1=BD,∠DBF=60°,
∴△DBF是等边三角形,
∴DF=BF=EF,∠DFB=60°,
∵∠BFD=∠FED+∠FDE,
∴∠FDE=∠FED=30°
∴∠EDB=180°-DEB∠DBE-∠DEB=90°,
∴DE=$\sqrt{B{E}^{2}-B{D}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$.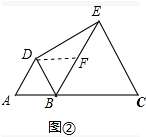
(3)解:如图③中,连接DC,
∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,
$\left\{\begin{array}{l}{AB=BD}\\{∠ABE=∠DBC}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△DBC,
∴AE=DC.
∵DE2+BE2=AE2,BE=CE,
∴DE2+CE2=CD2,
∴∠DEC=90°,
∵∠BEC=60°,
∴∠DEB=∠DEC-∠BEC=30°.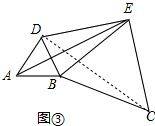
点评 本题考查全等三角形的判定和性质、勾股定理以及勾股定理逆定理、等边三角形的性质等知识,寻找全等三角形是解决问题的关键,学会添加辅助线的方法,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
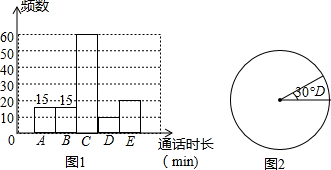 现如今,收集已成为人们普遍的交流工具,人们用它来打电话、上网.为了解3月份某单位职工的本地通话时长,随机抽取了该单位职工的通话时长进行抽样调查,将调查结果分成为A,B,C,D五个组,并利用所得数据绘制了如图1所示的频数分布直方图和如图2所示的不完整的扇形统计图.
现如今,收集已成为人们普遍的交流工具,人们用它来打电话、上网.为了解3月份某单位职工的本地通话时长,随机抽取了该单位职工的通话时长进行抽样调查,将调查结果分成为A,B,C,D五个组,并利用所得数据绘制了如图1所示的频数分布直方图和如图2所示的不完整的扇形统计图. | 组别 | 通话时长(min) |
| A | x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x>400 |
(1)根据图1中的信息,补充完整图2的扇形统计图:统计图中标注角度:(要求:画图前先求角,画图可借助任何工具,图中小于180°的所有角都需要用尺规作图,保留作图痕迹,不写作法)
(2)调查数据中,职工的通话时长的众数在C组,通话时长小于300min的职工占调查总人数的75%.
(3)该单位的职工小王,他收集所办理的通话套餐是月租5元,可免费拨打电话100min,超过100min时,每分钟的花费为0.15元,3月份小王花费总额超过42.5元,试判断小王可能属于调查结果中的哪一组?
 如图,在?ABCD中,点F在边AD上,BF交AC于点E,过点E作EG∥BC交AB于点G,若AF:FD=2:1,求GE:BC的值.
如图,在?ABCD中,点F在边AD上,BF交AC于点E,过点E作EG∥BC交AB于点G,若AF:FD=2:1,求GE:BC的值.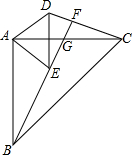 如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.
如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F. 如图,直线a,b相交于点O,则∠1的度数为135°.
如图,直线a,b相交于点O,则∠1的度数为135°.