题目内容
6.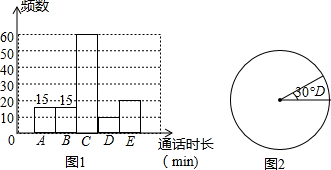 现如今,收集已成为人们普遍的交流工具,人们用它来打电话、上网.为了解3月份某单位职工的本地通话时长,随机抽取了该单位职工的通话时长进行抽样调查,将调查结果分成为A,B,C,D五个组,并利用所得数据绘制了如图1所示的频数分布直方图和如图2所示的不完整的扇形统计图.
现如今,收集已成为人们普遍的交流工具,人们用它来打电话、上网.为了解3月份某单位职工的本地通话时长,随机抽取了该单位职工的通话时长进行抽样调查,将调查结果分成为A,B,C,D五个组,并利用所得数据绘制了如图1所示的频数分布直方图和如图2所示的不完整的扇形统计图. | 组别 | 通话时长(min) |
| A | x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x>400 |
(1)根据图1中的信息,补充完整图2的扇形统计图:统计图中标注角度:(要求:画图前先求角,画图可借助任何工具,图中小于180°的所有角都需要用尺规作图,保留作图痕迹,不写作法)
(2)调查数据中,职工的通话时长的众数在C组,通话时长小于300min的职工占调查总人数的75%.
(3)该单位的职工小王,他收集所办理的通话套餐是月租5元,可免费拨打电话100min,超过100min时,每分钟的花费为0.15元,3月份小王花费总额超过42.5元,试判断小王可能属于调查结果中的哪一组?
分析 (1)先计算出调查的总人数,再用360°分别乘以各组所占的百分比得到它们在扇形统计图中对应扇形的圆心角,然后利用基本作图作出各扇形;
(2)根据众数定义可判断职工的通话时长的众数在C组;用A、B、C三组的频数除以总人数即可得到通话时长小于300min的职工占调查总人数的百分比;
(3)设小王3月份的通话时长为xmin,利用分段计费列不等式,然后解不等式,再利用x的范围判断小王可能属于调查结果中的哪一组.
解答 解:(1)调查的总人数为10÷$\frac{30}{360}$=120,
A组或B组在扇形统计图中对应的圆心角的度数为360°×$\frac{15}{120}$=45°;
C组在扇形统计图中对应的圆心角的度数为360°×$\frac{60}{120}$=180°;
E组在扇形统计图中对应的圆心角的度数为360°×$\frac{20}{120}$=60°;
如图,
(2)职工的通话时长的众数在C组,通话时长小于300min的职工占调查总人数的百分比为$\frac{15+15+60}{120}$×100%=75%;
故答案为C;75;
(3)设小王3月份的通话时长为xmin,根据题意得5+0.15(x-100)>42.5,解得x>350,
所以小王可能属于调查结果中的D组,也可能属于调查结果中的E组.
点评 本题考查了频(数)率分布直方图:提高读频数分布直方图的能力和利用统计图获取信息的能力.也考查了扇形统计图、基本作图和众数的定义.

练习册系列答案
相关题目
18.下列各组3个整数是勾股数的是( )
| A. | 4,5,6 | B. | 6,8,9 | C. | 13,14,15 | D. | 8,15,17 |
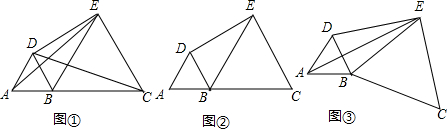
 已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a.
已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a.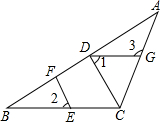 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.