题目内容
18.已知x=-1是方程6(2x+m)=3m-6的解,求关于x的方程mx+2=m(1-2x)的解.分析 把x=-1代入已知方程计算求出m的值,确定出所求方程,求出解即可.
解答 解:把x=-1代入方程得:6(-2+m)=3m-6,
去括号得:-12+6m=3m-6,
移项合并得:3m=6,
解得:m=2,
把m=2代入所求方程得:2x+2=2(1-2x),
去括号得:2x+2=2-4x,
移项合并得:6x=0,
解得:x=0.
点评 此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6.已知(m2-4)x2-(m+2)x+8=0是关于未知数x的一元一次方程,求代数式-199(m+x)(m-2x)+m的值( )
| A. | 1592 | B. | 1593 | C. | 1594 | D. | 1595 |
3.若最简二次根式$\sqrt{2m-1}$与$\sqrt{3m-9}$可以合并,则m=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
10.抛物线的对称轴为直线x=3,y的最大值为-5,且与y=$\frac{1}{2}$x2的图象开口大小相同.则这条抛物线解析式为( )
| A. | y=-$\frac{1}{2}$(x+3)2+5 | B. | y=-$\frac{1}{2}$(x-3)2-5 | C. | y=$\frac{1}{2}$(x+3)2+5 | D. | y=$\frac{1}{2}$(x-3)2-5 |
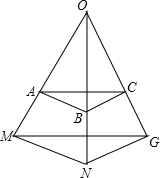 如图,已知AB∥MN,BC∥NG.求证:$\frac{OA}{OM}$=$\frac{OC}{OG}$.
如图,已知AB∥MN,BC∥NG.求证:$\frac{OA}{OM}$=$\frac{OC}{OG}$.