题目内容
如图,点A是双曲线 与直线y=-x-(k+1)在第二象限内的交点,AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限内的交点,AB⊥x轴于B,且S△ABO= .
.

(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
(3)写出当一次函数值大于反比例函数值时,x取值范围?
(1)反比例函数的解析式是:y=- ,一次函数的解析式是:y=-x+2;(2)A的坐标是(-1,3),C的坐标是(3,-1).4;(3) x<-1或0<x<3.
,一次函数的解析式是:y=-x+2;(2)A的坐标是(-1,3),C的坐标是(3,-1).4;(3) x<-1或0<x<3.
【解析】
试题分析:(1)由S△ABO= ,根据反比例函数的系数k几何意义,即可求出k的值;
,根据反比例函数的系数k几何意义,即可求出k的值;
(2)将两函数解析式组成方程组,求出方程组的解即为交点坐标,结合A、C的坐标,利用三角形的面积公式即可求出S△AOC;
(3)根据函数的图象即可直接写出答案.
试题解析:(1)∵S△ABO= .
.
∴k=-3,
则反比例函数的解析式是:y=- ,一次函数的解析式是:y=-x+2;
,一次函数的解析式是:y=-x+2;
(2)解方程组
 ,
,
解得: 或
或 ,
,
则A的坐标是(-1,3),C的坐标是(3,-1).
在y=-x+2中,令x=0,解得:y=2,
则S△AOC= ×2×1+
×2×1+ ×2×3=4;
×2×3=4;
(3)x的范围是:x<-1或0<x<3.
考点:反比例函数与一次函数的交点问题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 -
- -︱-5︱
-︱-5︱ 
 的图象经过点B(
的图象经过点B( ,0),且与反比例函数
,0),且与反比例函数 (
( 为不等于0的常数)的图象在第一象限交于点
为不等于0的常数)的图象在第一象限交于点 (1,
(1, ).求:
).求:
 时,反比例函数
时,反比例函数 的取值范围.
的取值范围.  ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )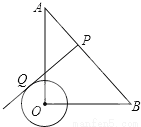
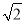 C.
C.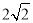 D.
D.