题目内容
 如图,△ABC中,AB=AC,D、E、F分别是BC、AC、AB边上的中点,连接DE、DF.
如图,△ABC中,AB=AC,D、E、F分别是BC、AC、AB边上的中点,连接DE、DF.(1)求证:四边形AFDE是菱形;
(2)当∠ABC等于多少度时,四边形AFDE是正方形?说明理由.
考点:正方形的判定,三角形中位线定理,菱形的判定
专题:
分析:(1)首先利用平行四边形的判定得出四边形AFDE是平行四边形,再利用菱形的判定得出即可;
(2)利用有一个角是90度的菱形是正方形进而得出即可.
(2)利用有一个角是90度的菱形是正方形进而得出即可.
解答:(1)证明:∵E、F分别是BC、AC、AB边上的中点,
∴DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,
∵AB=AC,E、F分别是BC、AC、AB边上的中点,
∴AF=AE,
∴平行四边形AFDE是菱形;
(2)解:当∠ABC=45°时,四边形AFDE是正方形,
理由:∵AB=AC,
∴∠ABC=∠C=45°,
∴∠A=90°,
∴菱形AFDE是正方形.
∴DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,
∵AB=AC,E、F分别是BC、AC、AB边上的中点,
∴AF=AE,
∴平行四边形AFDE是菱形;
(2)解:当∠ABC=45°时,四边形AFDE是正方形,
理由:∵AB=AC,
∴∠ABC=∠C=45°,
∴∠A=90°,
∴菱形AFDE是正方形.
点评:此题主要考查了菱形的判定以及正方形的判定,熟练掌握菱形与正方形的关系是解题关键.

练习册系列答案
相关题目
下列图案中,既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列二次根式中与
是同类二次根式的是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在平面直角坐标系中,描出下列各点,并将各点用线段依次连接起来:(2,1)(6,1)(6,3)(7,3)(4,6)(1,3)(2,3)观察得到的图形,你觉得它像什么?
在平面直角坐标系中,描出下列各点,并将各点用线段依次连接起来:(2,1)(6,1)(6,3)(7,3)(4,6)(1,3)(2,3)观察得到的图形,你觉得它像什么? 请阅读下面的材料,并回答所提出的问题.
请阅读下面的材料,并回答所提出的问题. 已知:如图,直线AB、AC、BC两两相交于A、B、C三点,BE⊥AC于E,FG⊥AC于G,DE交AB于D,且∠1=∠2,求证:∠ADE=∠ABC.
已知:如图,直线AB、AC、BC两两相交于A、B、C三点,BE⊥AC于E,FG⊥AC于G,DE交AB于D,且∠1=∠2,求证:∠ADE=∠ABC.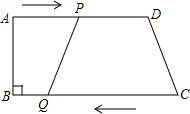 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边以1cm/s的速度向点D运动,动点Q从C点开始沿CB边以3cm/s的速度向点B运动,P,Q分别从A,C同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.设运动的时间为t(s).
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边以1cm/s的速度向点D运动,动点Q从C点开始沿CB边以3cm/s的速度向点B运动,P,Q分别从A,C同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.设运动的时间为t(s).