Question

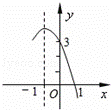
已知二次函数y=ax²+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax²+bx+c﹣m=0没有实数根，有下列结论：

①b²﹣4ac＞0；②abc＜0；③m＞2．

其中，正确结论的个数是（　　）

　 A． 0 B． 1 C． 2 D． 3

　

Answer 1

D

考点： 二次函数图象与系数的关系． 

专题： 压轴题；数形结合．

分析： 由图象可知二次函数y=ax²+bx+c与x轴有两个交点，进而判断①；

先根据抛物线的开口向下可知a＜0，由抛物线与y轴的交点判断c与0的关系，根据对称轴在y轴右侧得出b与0的关系，然后根据有理数乘法法则判断②；

一元二次方程ax²+bx+c﹣m=0没有实数根，则可转化为ax²+bx+c=m，即可以理解为y=ax²+bx+c和y=m没有交点，即可求出m的取值范围，判断③即可．

解答： 解：①∵二次函数y=ax²+bx+c与x轴有两个交点，

∴b²﹣4ac＞0，故①正确；

②∵抛物线的开口向下，

∴a＜0，

∵抛物线与y轴交于正半轴，

∴c＞0，

∵对称轴x=﹣＞0，

∴ab＜0，

∵a＜0，

∴b＞0，

∴abc＜0，故②正确；

③∵一元二次方程ax²+bx+c﹣m=0没有实数根，

∴y=ax²+bx+c和y=m没有交点，

由图可得，m＞2，故③正确．

故选：D．