题目内容
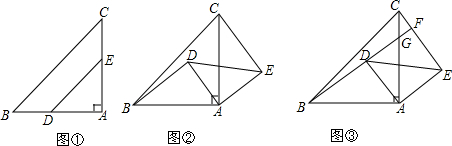
15.如图,在△ABC中,∠A=90°,AB=AC,点D、E分别在边AB、AC上(点D不与点A、B重合),且AD=AE,连结DE.问题原型:将图①中△ADE绕点A顺时针旋转α(0°<α<90°).如图②,求证:△ABD≌△ACE.
初步探究:在问题原型的条件下,延长BD交直线AC于点G,交直线CE于点F,请利用图③探究BF⊥CE是否成立,并说明理由.
简单应用:在问题原型的条件下,当AB=$\sqrt{3}$,AD=1时,若AD∥CE,则CF的长为$\sqrt{2}$-1.
分析 问题原型:根据旋转的性质和已知,运用SAS证明即可;
初步探究:由问题原型中的结论:△ABD≌△ACE得出∠ABD=∠ACE,结合等量代换进行求解即可;
简单应用:运用AD∥CE结合初步探究中的结论,可证AD⊥BG,结合射影定理和勾股定理和相似的性质即可求解.
解答 解:问题原型如图②,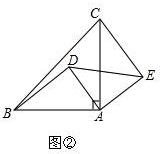
由旋转的性质可知,∠BAD=∠CAE,
又∵AB=AC,AD=AE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE;
初步探究:如图③,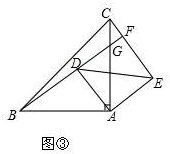
由问题原型可知,△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠ABD+∠DGA=90°,∠DGA=∠CGF,
∴∠CGF+∠ACE=90°,
∴BF⊥CE;
简单应用:如图③,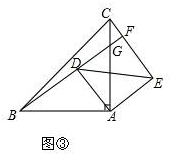
由初步探究可知,BF⊥CE,
∵AD∥CE,
∴AD⊥BG,
∵∠BAG=90°,AB=$\sqrt{3}$,AD=1,
∴勾股定理和由射影定理可求:
BD=$\sqrt{2}$,DG=$\frac{\sqrt{2}}{2}$,AG=$\frac{\sqrt{6}}{2}$,
∵△ABD≌△ACE,
∴AC=AB=$\sqrt{3}$,
∴CG=$\sqrt{3}$-$\frac{\sqrt{6}}{2}$,
由AD∥CE易证△ADG∽△CFG,
∴$\frac{CF}{AD}=\frac{CG}{AG}$,
解得:CF=$\sqrt{2}$-1.
故答案为:$\sqrt{2}$-1.
点评 此题主要考查几何变换中的旋转,熟悉旋转的性质,会证明三角形全等,并应用全等三角形的性质解决角的问题,会运用射影定理和勾股定理和相似求线段长度是解题的关键.

练习册系列答案
相关题目
7.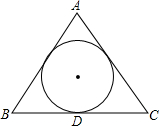 如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
 如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )| A. | 9$\sqrt{3}$ | B. | 18 | C. | 18$\sqrt{3}$ | D. | 54 |
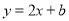 (b为常数)的图象位于
(b为常数)的图象位于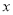 轴下方的部分沿
轴下方的部分沿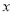 轴翻折至其上方后,所得的折线是函数
轴翻折至其上方后,所得的折线是函数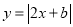 (b为常数)的图象.若该图象在直线y=2下方的点的横坐标
(b为常数)的图象.若该图象在直线y=2下方的点的横坐标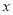 满足
满足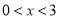 ,则b的取值范围为____.
,则b的取值范围为____. 如图1,在平面直角坐标系中,已知A(a,a),B(2a,0),M($\frac{1}{2}$a,0),∠MAN=45°,将△OAM绕A逆时针旋转90°.
如图1,在平面直角坐标系中,已知A(a,a),B(2a,0),M($\frac{1}{2}$a,0),∠MAN=45°,将△OAM绕A逆时针旋转90°.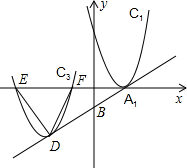 如图,抛物线C1:y=(x-2)2,直线l:y=$\frac{1}{2}$x-1,顶点为A1,l与y轴交于B点,将C1沿A1B方向平移n个单位的C3,且C3的顶点及x轴的两个交点为顶点的三角形为正三角形,求n.
如图,抛物线C1:y=(x-2)2,直线l:y=$\frac{1}{2}$x-1,顶点为A1,l与y轴交于B点,将C1沿A1B方向平移n个单位的C3,且C3的顶点及x轴的两个交点为顶点的三角形为正三角形,求n.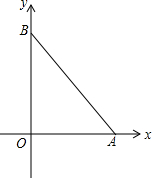 如图,在平面直角坐标系中,已知点A(3,0),点B(0,4),将线段AB绕点A按顺时针方向旋转得线段AB1,已知BB1和x轴平行.
如图,在平面直角坐标系中,已知点A(3,0),点B(0,4),将线段AB绕点A按顺时针方向旋转得线段AB1,已知BB1和x轴平行.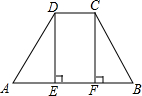 如图,AB∥CD,DE⊥AB,CF⊥AB.求证:四边形DEFC是矩形.
如图,AB∥CD,DE⊥AB,CF⊥AB.求证:四边形DEFC是矩形.