题目内容
20.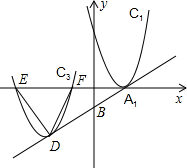 如图,抛物线C1:y=(x-2)2,直线l:y=$\frac{1}{2}$x-1,顶点为A1,l与y轴交于B点,将C1沿A1B方向平移n个单位的C3,且C3的顶点及x轴的两个交点为顶点的三角形为正三角形,求n.
如图,抛物线C1:y=(x-2)2,直线l:y=$\frac{1}{2}$x-1,顶点为A1,l与y轴交于B点,将C1沿A1B方向平移n个单位的C3,且C3的顶点及x轴的两个交点为顶点的三角形为正三角形,求n.
分析 作DH⊥EF,如图,A(2,0),利用一次函数图象上点的坐标特征,设D点坐标为(t,$\frac{1}{2}$t-1),利用顶点式得到抛物线C3的解析式,再利用抛物线与x轴的交点问题表示出E点和F点坐标,从而得到EF的长,然后利用等边三角形的性质利用DH=$\frac{\sqrt{3}}{2}$EF得到关于t的方程,再解方程求出t的值,最后根据两点间的距离公式计算n的值.
解答 解:作DH⊥EF,如图,A(2,0),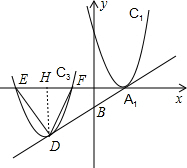
设D点坐标为(t,$\frac{1}{2}$t-1),则抛物线C3的解析式为y=(x-t)2+$\frac{1}{2}$t-1,
当y=0时,(x-t)2+$\frac{1}{2}$t-1=0,解得x1=t+$\sqrt{1-\frac{1}{2}t}$,x2=t-$\sqrt{1-\frac{1}{2}t}$,则E(t-$\sqrt{1-\frac{1}{2}t}$,0),F(t+$\sqrt{1-\frac{1}{2}t}$,0),
所以EF=t+$\sqrt{1-\frac{1}{2}t}$-(t-$\sqrt{1-\frac{1}{2}t}$)=2$\sqrt{1-\frac{1}{2}t}$,
因为△DEF为等边三角形,
所以DH=$\frac{\sqrt{3}}{2}$EF,即1-$\frac{1}{2}$t=$\frac{\sqrt{3}}{2}$×2$\sqrt{1-\frac{1}{2}t}$,解得t1=2(舍去),t2=-4,则D(-4,-3),
所以A1D=$\sqrt{(2+4)^{2}+{3}^{2}}$=3$\sqrt{5}$,
即n的值为3$\sqrt{5}$.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.解决本题的关键是求出平移后抛物线的顶点D的坐标.

 七彩题卡口算应用一点通系列答案
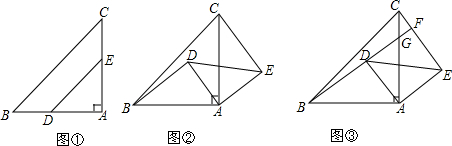
七彩题卡口算应用一点通系列答案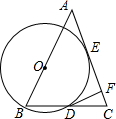 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.(1)求DC的长;(2)求AB的长.
 若实数a,b在数轴上的位置如图所示,则$\frac{b+1}{a+1}+\frac{b}{a}$的结果是( )
若实数a,b在数轴上的位置如图所示,则$\frac{b+1}{a+1}+\frac{b}{a}$的结果是( )| A. | 正数 | B. | 零 | C. | 负数 | D. | 非正数 |
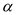 =
=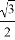 ,且
,且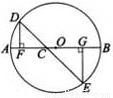
 B.
B.  C.
C.  D.
D. 
 已知?ABCD,AC与BD相交于点O.
已知?ABCD,AC与BD相交于点O.