题目内容
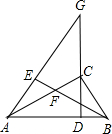 如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,G是DC延长线上一点,过B作BE⊥AG,垂足为E,交CD于点F.求证:CD2=DF•DG.
如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,G是DC延长线上一点,过B作BE⊥AG,垂足为E,交CD于点F.求证:CD2=DF•DG.考点:相似三角形的判定与性质
专题:证明题
分析:先证明△ADG∽△FDB,可得
=
,可得AD•BD=DF•DG,再证明△ADC∽△CDB,可得到AD•BD=CD2,可得结论.
| AD |
| DF |
| DG |
| DB |
解答:证明:∵CD⊥AB,BE⊥AG,
∴∠GED=∠BDF,
∴∠G=∠DBF,且∠ADG=∠FDB,
∴△ADG∽△FDB,
∴
=
,即AD•BD=DF•DG,
∵∠ACB=90°,∠CDB=90°,
∴∠ACD+∠DCB=∠CAD+∠ACD,
∴∠CAD=∠DCB,
∴△ADC∽△CDB,
∴
=
,即AD•BD=CD2,
∴CD2=DF•DG.
∴∠GED=∠BDF,
∴∠G=∠DBF,且∠ADG=∠FDB,
∴△ADG∽△FDB,
∴
| AD |
| DF |
| DG |
| DB |
∵∠ACB=90°,∠CDB=90°,
∴∠ACD+∠DCB=∠CAD+∠ACD,
∴∠CAD=∠DCB,
∴△ADC∽△CDB,
∴
| AD |
| CD |
| CD |
| BD |
∴CD2=DF•DG.
点评:本题主要考查三角形相似的判定和性质,利用条件找到DF•DG与AD•BD及CD2与AD•BD的关系是解题的关键.

练习册系列答案
相关题目
若等腰三角形的周长为60cm,底边长为x cm,一腰长为y cm,则y与x的函数关系式及自变量x的取值范围是( )
| A、y=60-2x(0<x<60) | ||
| B、y=60-2x(0<x<30) | ||
C、y=
| ||
D、y=
|
 如图,AF平分∠BAC,FD⊥BD.
如图,AF平分∠BAC,FD⊥BD. 如图,已知△ABC和△ECD都是直角等腰三角形,∠ACB=∠DCE=90°,若∠ACD=30°,求∠AED的度数.
如图,已知△ABC和△ECD都是直角等腰三角形,∠ACB=∠DCE=90°,若∠ACD=30°,求∠AED的度数. 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.
如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,AD和CE是高,它们相交于点H,求证:EH=EB.