题目内容
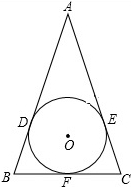 如图,圆O是△ABC的内切圆,切点分别为D,E,F,AB=AC=13,BC=10,求圆O的半径.
如图,圆O是△ABC的内切圆,切点分别为D,E,F,AB=AC=13,BC=10,求圆O的半径.考点:三角形的内切圆与内心
专题:
分析:连接AF,则AF⊥BC,利用勾股定理求得AF的长,即三角形的高,求得△ABC的面积,然后根据△ABC的面积=
×△ABC的周长×圆的半径,即可求解.
| 1 |
| 2 |
解答:解:连接AF,则AF⊥BC,
在直角△ABF中,BF=
BC=
×10=5,
则AF=
=
=12,
则S△ABC=
BC•AF=
×10×12=60,
设圆O的半径的半径是r,则
(13+13+10)•r=60,
解得:r=
=
.
在直角△ABF中,BF=
| 1 |
| 2 |
| 1 |
| 2 |
则AF=
| AB2-BF2 |
| 132-52 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
设圆O的半径的半径是r,则
| 1 |
| 2 |
解得:r=
| 60 |
| 18 |
| 10 |
| 3 |
点评:本题考查了三角形的内切圆的计算,理解△ABC的面积=
×△ABC的周长×内切圆的半径,是关键.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
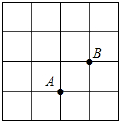 已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在格点上,位置如图,点C也在格点上,且△ABC为等腰三角形,则点C的个数为( )
已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在格点上,位置如图,点C也在格点上,且△ABC为等腰三角形,则点C的个数为( )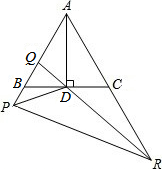 如图,在等边△ABC中,AD⊥BC于D,点P在AB的延长线上,点Q在AB上,∠PDQ=60°,QD的延长线交AC的延长线于R(PB<CR).若AB=4,PR=7,则PQ=
如图,在等边△ABC中,AD⊥BC于D,点P在AB的延长线上,点Q在AB上,∠PDQ=60°,QD的延长线交AC的延长线于R(PB<CR).若AB=4,PR=7,则PQ= 已知线段a,b,c.
已知线段a,b,c.