题目内容
11.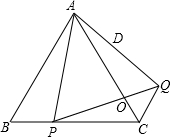 如图,已知等边△ABC的边长为a,点P是BC边上一动点,以AP为边作等边△APQ,边PQ交AC于点O,连接CQ,
如图,已知等边△ABC的边长为a,点P是BC边上一动点,以AP为边作等边△APQ,边PQ交AC于点O,连接CQ,(1)求证:△ABP≌△ACQ;
(2)若点D是AQ的中点,当点P由点B运动到点C时,点D运动路线的长为$\frac{1}{2}$a(直接写出结果);
(3)当BP=$\frac{1}{3}$a时,求$\frac{AP}{PO}$的值.
分析 (1)先根据等边三角形的性质得出∠BAC=∠PAQ=60°,AB=AC,AP=AQ,再由SAS定理即可得出结论;
(2)直接根据三角形中位线定理即可得出结论;
(3)先根据题意得出∠BAP=∠CPO,再由∠B=∠PCO可知△ABP∽△PCO,由相似三角形的对应边成比例即可得出结论.
解答 (1)证明:∵△ABC与△APQ是等边三角形,
∴∠BAC=∠PAQ=60°,AB=AC,AP=AQ,
∴∠BAP=∠QAC,
在△ABP与△ACQ中,
$\left\{\begin{array}{l}AB=AC\\∠BAP=∠CAQ\\ AP=AQ\end{array}\right.$,
∴△ABP≌△ACQ(SAS);
(2)解:∵当点P由点B运动到点C时,D为AQ的中点,
∴PD的运动路线为△ACQ的中位线即为$\frac{1}{2}$a.
故答案为:$\frac{1}{2}$a;
(3)解:∵∠APC=60°+∠CPQ,∠APC=∠B+∠BAP=60°+∠BAP,
∴∠BAP=∠CPO.
∵∠B=∠PCO,
∴△ABP∽△PCO,
∴$\frac{AB}{PC}$=$\frac{AP}{OP}$=$\frac{a}{a-\frac{1}{3}a}$=$\frac{3}{2}$,
∴$\frac{AP}{PO}$=$\frac{3}{2}$.
点评 本题考查的是相似形综合题,涉及到等边三角形的性质、全等三角形的判定定理、相似三角形的判定与性质等知识,难度适中.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
3. 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是( )
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是( )
 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是( )
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是( )| A. | PD=DQ | B. | DE=$\frac{1}{2}$AC | C. | AE=$\frac{1}{2}$CQ | D. | PQ⊥AB |
1.下列各式中最简二次根式为( )
| A. | $\sqrt{\frac{2}{5}}$ | B. | $\sqrt{x^2}$ | C. | $\sqrt{0.3}$ | D. | $\sqrt{3}$ |
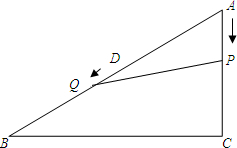 在Rt△ABC中,AC=6cm,BC=8cm,点P由点A出发,沿AC方向运动,速度为2cm/s;同时点Q由AB中点D出发,沿DB向B运动,速度为1cm/s;连接PQ,若设运动时间为t(s) (0<t≤3).
在Rt△ABC中,AC=6cm,BC=8cm,点P由点A出发,沿AC方向运动,速度为2cm/s;同时点Q由AB中点D出发,沿DB向B运动,速度为1cm/s;连接PQ,若设运动时间为t(s) (0<t≤3). 如图,△ABC与△BEF都是等边三角形,D是BC上一点,且CD=BE,求证:∠EDB=∠CAD.
如图,△ABC与△BEF都是等边三角形,D是BC上一点,且CD=BE,求证:∠EDB=∠CAD.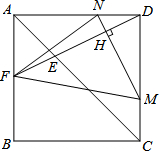 如图,正方形ABCD中,AB=a(单位:cm),点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.点M从点C出发,以1cm/s的速度沿CD向点D运动,点E从点A出发,以$\sqrt{2}$cm/s速度沿AC向点C运动,运动时间为t(t>0);下列判断正确的是( )
如图,正方形ABCD中,AB=a(单位:cm),点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.点M从点C出发,以1cm/s的速度沿CD向点D运动,点E从点A出发,以$\sqrt{2}$cm/s速度沿AC向点C运动,运动时间为t(t>0);下列判断正确的是( )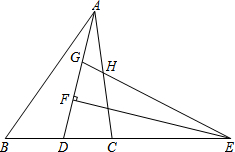 如图,在△ABC中,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.
如图,在△ABC中,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.