题目内容
7.计算:(1)(2m+3)(2m-3);
(2)x(x+1)+(2-x)(2+x);
(3)(3x-y)(3x+y)+y(x+y);
(4)(a+$\frac{1}{2}$b)(a-$\frac{1}{2}$b)-(3a-2b)(3a+2b)
分析 (1)根据平方差公式,求出算式(2m+3)(2m-3)的值是多少即可.
(2)根据整式的混合运算顺序,首先计算乘法,然后计算加法,求出算式x(x+1)+(2-x)(2+x)的值是多少即可.
(3)根据整式的混合运算顺序,首先计算乘法,然后计算加法,求出算式(3x-y)(3x+y)+y(x+y)的值是多少即可.
(4)根据整式的混合运算顺序,首先计算乘法,然后计算减法,求出算式(a+$\frac{1}{2}$b)(a-$\frac{1}{2}$b)-(3a-2b)(3a+2b)的值是多少即可.
解答 解:(1)(2m+3)(2m-3)
=(2m)2-9
=4m2-9
(2)x(x+1)+(2-x)(2+x)
=x2+x+4-x2
=x+4
(3)(3x-y)(3x+y)+y(x+y)
=9x2-y2+xy+y2
=9x2+xy
(4)(a+$\frac{1}{2}$b)(a-$\frac{1}{2}$b)-(3a-2b)(3a+2b)
=a2-$\frac{1}{4}$b2-9a2+4b2
=-8a2+$\frac{15}{4}$b2
点评 此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
相关题目
15.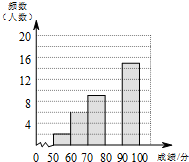 为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)a=18,b=0.18;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
 为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 2 | 0.04 |
| 60≤x<70 | 6 | 0.12 |
| 70≤x<80 | 9 | b |
| 80≤x<90 | a | 0.36 |
| 90≤x≤100 | 15 | 0.30 |
(1)a=18,b=0.18;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
12.计算(-4a-1)(-4a+1)的结果为( )
| A. | 16a2-1 | B. | -8a2-1 | C. | -4a2+1 | D. | -16a2+1 |
19.-(-x)2(-x3)(-x)3÷x8(x≠0)的结果是( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2x8 |
17.若反比例函数y=$\frac{k}{x}$的图象经过点(-1,2),则这个反比例函数的图象还经过点( )
| A. | (2,-1) | B. | (-$\frac{1}{2}$,1) | C. | (-2,-1) | D. | ($\frac{1}{2}$,2) |