题目内容
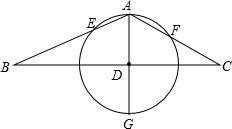 如图,由△ABC的顶点A作高AD,以垂足D为圆心,AD为半径作圆,分别交AB、AC于EF,若AE=2,AF=3,AB=5,求AC的长.
如图,由△ABC的顶点A作高AD,以垂足D为圆心,AD为半径作圆,分别交AB、AC于EF,若AE=2,AF=3,AB=5,求AC的长.考点:相似三角形的判定与性质,圆周角定理
专题:
分析:过D分别作DM⊥AB,DN⊥AC,则可得到AD2=AM•AB,AD2=AN•AC,结合垂径定理可得AM=
AE,AN=
AF,代入可求得AC.
| 1 |
| 2 |
| 1 |
| 2 |
解答: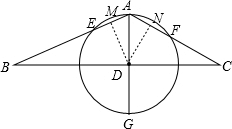 解:过D分别作DM⊥AB,DN⊥AC,
解:过D分别作DM⊥AB,DN⊥AC,
∵AD⊥BC,
∴∠AMD=∠ADB=90°,
∴∠MAD+∠ADM=∠B+∠MAD,
∴∠ADM=∠B,
∴△ADM∽△ABD,
∴
=
,
∴AD2=AM•AB,
同理可得AD2=AN•AC,
∴AM•AB=AN•AC,
又由垂径定理可得AM=
AE=1,AN=
AF=1.5,
∴1×5=1.5AC,
解得AC=
.
 解:过D分别作DM⊥AB,DN⊥AC,
解:过D分别作DM⊥AB,DN⊥AC,∵AD⊥BC,
∴∠AMD=∠ADB=90°,
∴∠MAD+∠ADM=∠B+∠MAD,
∴∠ADM=∠B,
∴△ADM∽△ABD,
∴
| AD |
| AB |
| AM |
| AD |
∴AD2=AM•AB,
同理可得AD2=AN•AC,
∴AM•AB=AN•AC,
又由垂径定理可得AM=
| 1 |
| 2 |
| 1 |
| 2 |
∴1×5=1.5AC,
解得AC=
| 10 |
| 3 |
点评:本题主要考查相似三角形的判定和性质,构造三角形相似得到AD2=AM•AB和AD2=AN•AC是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论: 如图,以Rt△ABC(∠ACB=90°)的三边为边长分别向外作正方形ABDE、BCGF、ACHM,连接DF、EM、GH.已知AB=5,BC=3,求六边形DEMHGF的面积.
如图,以Rt△ABC(∠ACB=90°)的三边为边长分别向外作正方形ABDE、BCGF、ACHM,连接DF、EM、GH.已知AB=5,BC=3,求六边形DEMHGF的面积.