题目内容
4.爸爸给双胞胎兄弟小明和小强带回一张篮球比赛门票,兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球,各自设计一种游戏确定谁去.小明:A袋中放着分别标有数字1、2、3的三个小球,B袋中放着分别标有数字4、5 的两个小球,且都已各自搅匀,小强蒙上眼睛从两个口袋中各取出1个小球,若两个小球上的数字之积为偶数,则小明得到门票;若积为奇数,则小强得到门票.
小强:口袋中放着分别标有数字1、2、3的三个小球,且已搅匀,小明、小强各蒙上眼睛有放回地摸1次,小明摸到偶数就记2分,摸到奇数记0分;小强摸到奇数就记1分,摸到偶数记0分,积分多的就得到门票(若积分相同,则重复第二次).
(1)小明设计的游戏方案对双方是否公平?请你运用列表或树状图说明理由;
(2)小强设计的游戏方案对双方是否公平?不必说理.
分析 游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
解答 解:(1)小明的设计游戏方案不公平,
可能出现的所有结果列表如下:
| A袋 积 B袋 | 1 | 2 | 3 |
| 4 | 4 | 8 | 12 |
| 5 | 5 | 10 | 15 |

∴P(小明得到门票)=P(积为偶数)=$\frac{4}{6}=\frac{2}{3}$,
P(小强得到门票)=P(积为奇数)=$\frac{1}{3}$,
∵$\frac{2}{3}$≠$\frac{1}{3}$,∴小强的设计方案不公平;
(2)小强的设计方案不公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
14.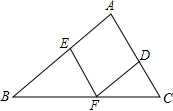 如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,EF∥AC,DF∥AB,若∠B=45°,∠C=65°,则∠EFD的大小为( )
如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,EF∥AC,DF∥AB,若∠B=45°,∠C=65°,则∠EFD的大小为( )
 如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,EF∥AC,DF∥AB,若∠B=45°,∠C=65°,则∠EFD的大小为( )
如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,EF∥AC,DF∥AB,若∠B=45°,∠C=65°,则∠EFD的大小为( )| A. | 45° | B. | 70° | C. | 80° | D. | 100° |
15.某造纸厂生产甲、乙两种生活用纸的相关信息如下表,其中x(吨)表示甲、乙两种生活用纸的月产量,请根据表中的信息解答后面的问题:
(1)设该造纸厂每月生产甲、乙两种生活用纸的利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
| 种 品 价 目 | 出厂价(元/吨) | 成本价(元/吨) | 排污处理费 |
| 甲种生活用纸 | 4800 | 2200 | 200(元/吨) 每月还需支付设备管理、 维护费20000元 |
| 乙种生活用纸 | 7000-10x | 1600 | 400(元/吨) |
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
19.某天的最高气温是11℃,最低气温是-1℃,则这一天的最高气温与最低气温的差是( )
| A. | 2℃ | B. | -2℃ | C. | 12℃ | D. | -12℃ |
14.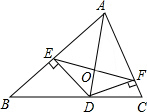 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是( )
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是( )
 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是( )
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是( )| A. | DE=DF | B. | AE=AF | C. | OD=OF | D. | OE=OF |
 一名儿童行走在如图所示的地板上,当他随意停下时,最终停在阴影部分的概率是$\frac{1}{3}$.
一名儿童行走在如图所示的地板上,当他随意停下时,最终停在阴影部分的概率是$\frac{1}{3}$.