题目内容
20．
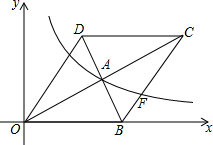如图，在平面直角坐标系中，菱形OBCD的边OB在x轴正半轴上，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过该菱形对角线的交点A，且与边BC交于点F．若点D的坐标为（6，8），则点A的坐标是（8，4）．
分析 由点D的坐标为（6，8），可求得菱形OBCD的边长，又由点A是BD的中点，求得点A的坐标．
解答 解：∵点D的坐标为（6，8），
∴OD=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∵四边形OBCD是菱形，
∴OB=OD=10，
∴点B的坐标为：（10，0），
∵AB=AD，即A是BD的中点，
∴点A的坐标为：（8，4），
故答案是：（8，4）．
点评 此题考查了菱形的性质、反比例函数的性质．此题利用了菱形的四条边都相等的性质求得边OB的长度是解题的难点．
练习册系列答案
相关题目
10．下列各题中，能用平方差公式的是（ ）
| A． | （a-2b）（-a+2b） | B． | （-a-2b）（-a-2b） | C． | （a-2b）（a+2b） | D． | （-a-2b）（a+2b） |
11．表格描述的是y与x之间的函数关系：
则m与n的大小关系是m＞n．
| x | … | -2 | 0 | 2 | 4 | … |
| y=kx+b | … | 3 | -1 | m | n | … |
作图题（只保留作图痕迹，不写作法）
15．某造纸厂生产甲、乙两种生活用纸的相关信息如下表，其中x（吨）表示甲、乙两种生活用纸的月产量，请根据表中的信息解答后面的问题：
（1）设该造纸厂每月生产甲、乙两种生活用纸的利润分别为y1元和y2元，分别求出y1和y2与x的函数关系式（注：利润=总收入-总支出）；
（2）若某月要生产甲、乙两种生活用纸共300吨，求该月生产甲、乙两种生活用纸各多少吨，获得的总利润最大？最大利润是多少？
| 种 品 价 目 | 出厂价（元/吨） | 成本价（元/吨） | 排污处理费 |
| 甲种生活用纸 | 4800 | 2200 | 200（元/吨） 每月还需支付设备管理、 维护费20000元 |
| 乙种生活用纸 | 7000-10x | 1600 | 400（元/吨） |
（2）若某月要生产甲、乙两种生活用纸共300吨，求该月生产甲、乙两种生活用纸各多少吨，获得的总利润最大？最大利润是多少？
5．
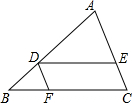如图，在△ABC中，D为AB上的一点，过点D作DE∥BC交AC于点E，过点D作DF∥AC交BC 于点F，则下列结论错误的是（ ）
如图，在△ABC中，D为AB上的一点，过点D作DE∥BC交AC于点E，过点D作DF∥AC交BC 于点F，则下列结论错误的是（ ）| A． | $\frac{AD}{DB}$=$\frac{DE}{BF}$ | B． | $\frac{DE}{BC}$=$\frac{AE}{AC}$ | C． | $\frac{AE}{CE}$=$\frac{BF}{CF}$ | D． | $\frac{CE}{AC}$=$\frac{BF}{BC}$ |