题目内容
15. 如图,△ACE是以平行四边形ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称,若点E的坐标是(5,$-2\sqrt{3}$),则点D的坐标是(4,0).
如图,△ACE是以平行四边形ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称,若点E的坐标是(5,$-2\sqrt{3}$),则点D的坐标是(4,0).
分析 首先设CE交x轴于点F,由点C与点E关于x轴对称.若点E的坐标是(5,-2$\sqrt{3}$),可求得点C的坐标,继而求得AC与BC的长,然后由三角函数的性质,求得AF的长,即可求得点A的坐标,继而求得答案.
解答 解:设CE交x轴于点F,如图所示:
∵点C与点E关于x轴对称,点E的坐标是(5,-2$\sqrt{3}$),
∴点C的坐标是(5,2$\sqrt{3}$),
∴AC=CE=4$\sqrt{3}$,OF=5,
∵AD∥BC,
∴点B(0,2$\sqrt{3}$),
∵△ACE是等边三角形,AD⊥CE,
∴∠CAD=30°,
∴AF=AC•cos30°=4$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=6,
∴OA=AF-OF=1,
∴点A(-1,0),
∵AD=BC=5,
∴OD=4,
∴点D的坐标为:(4,0).
故答案为:(4,0).
点评 此题考查了平行四边形的性质、等边三角形的性质以及点与坐标的性质.注意掌握平行四边形的对边平行且相等.

练习册系列答案
相关题目
10.将代数式x2-(2x+y-z)去掉括号后应为( )
| A. | x2-2x+y-z | B. | x2-2x-y+z | C. | x2+2x+y-z | D. | x2+2x-y+z |
 如图,已知A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE. 解不等式组,并把它们的解集在数轴上表示出来:
解不等式组,并把它们的解集在数轴上表示出来: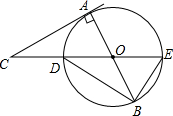 已知,如图,AB是⊙O的直径,CA与⊙O相切于点A,连接CO交⊙O于点D,CO的延长线交⊙O于点E,连接BE、BD,∠ABD=35°,则∠C=20度.
已知,如图,AB是⊙O的直径,CA与⊙O相切于点A,连接CO交⊙O于点D,CO的延长线交⊙O于点E,连接BE、BD,∠ABD=35°,则∠C=20度. 如图,P是直线l外一点,A,B,C三点在直线l上,且PB⊥l于点B,∠APC=90°,则下列结论:①线段AP是点A到直线PC的距离;②线段BP的长是点P到直线l的距离;③PA,PB,PC三条线段中,PB最短;④线段PC的长是点P到直线l的距离,其中,正确的是( )
如图,P是直线l外一点,A,B,C三点在直线l上,且PB⊥l于点B,∠APC=90°,则下列结论:①线段AP是点A到直线PC的距离;②线段BP的长是点P到直线l的距离;③PA,PB,PC三条线段中,PB最短;④线段PC的长是点P到直线l的距离,其中,正确的是( )