题目内容
a，b，c为非负实数，a2+b2+c2=1，a(
+
)+b(
+
)+c(
+
) =-3，求a+b+c的值．
| 1 |
| b |
| 1 |
| c |
| 1 |
| c |
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
考点：因式分解
专题：
分析：首先将原式变形，进而得出a（
+
+
）+b（
+
+
）+c（
+
+
）=0，得出a+b+c=0或bc+ac+ab=0．进而代入求出答案．
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
解答：解：将a(
+
)+b(
+
)+c(
+
) =-3变形如下，
a（
+
）+1+b（
+
）+1+c（
+
）+1=0，
即a（
+
+
）+b（
+
+
）+c（
+
+
）=0，
∴（a+b+c）（
+
+
）=0，
∴（a+b+c）•
=0，
∴a+b+c=0（舍）或bc+ac+ab=0．
若bc+ac+ab=0，则
（a+b+c）2=a2+b2+c2+2（bc+ac+ab）=a2+b2+c2=1，
∴a+b+c=±1．
∴a+b+c的值为1，-1．
| 1 |
| b |
| 1 |
| c |
| 1 |
| c |
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
a（
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
即a（
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
∴（a+b+c）（
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
∴（a+b+c）•
| bc+ac+ab |
| abc |
∴a+b+c=0（舍）或bc+ac+ab=0．
若bc+ac+ab=0，则
（a+b+c）2=a2+b2+c2+2（bc+ac+ab）=a2+b2+c2=1，
∴a+b+c=±1．
∴a+b+c的值为1，-1．
点评：此题主要考查了因式分解的应用，正确将已知变形得出（a+b+c）（
+
+
）=0是解题关键．
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
练习册系列答案
步步高达标卷系列答案
相关题目
如图，△ABC中，∠C=90°，AC=3，BC=4，AB的垂直平分线交AB于E，交BC于D，则BD的长为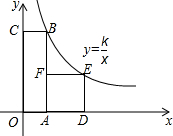
如图，四边形OABC是矩形，ADEF是正方形，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数y=