题目内容
已知两圆的半径分别是2cm和4cm，圆心距是5cm，那么这两圆的位置关系是（ ）
| A、外离 | B、外切 | C、相交 | D、内切 |
考点：圆与圆的位置关系
专题：
分析：由两圆的半径分别是2cm和4cm，圆心距是5cm，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．
解答：解：∵两圆的半径分别是2cm和4cm，
∴半径和为6cm，半径差为2cm，
∵圆心距是5cm，
∴这两圆的位置关系是：相交．
故选C．
∴半径和为6cm，半径差为2cm，
∵圆心距是5cm，
∴这两圆的位置关系是：相交．
故选C．
点评：此题考查了圆与圆的位置关系．此题比较简单，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．
练习册系列答案
相关题目
已知a，b，c是△ABC三边的长，外接圆的圆心在△ABC一条边上的是（ ）
| A、a=15，b=12，c=1 |
| B、a=5，b=12，c=12 |
| C、a=5，b=12，c=13 |
| D、a=5，b=12，c=14 |
已知抛物线的解析式为y=
(x-2)2+1，则该抛物线的顶点坐标是（ ）
| 1 |
| 2 |
| A、（2，1） |
| B、（-2，1） |
| C、（2，-1） |
| D、（1，2） |
下列函数中，是二次函数的是（ ）
| A、y=3x-1 | ||
| B、y=3x3-x2 | ||
C、y=1-x-
| ||
D、y=x2+
|
顶点为（5，0）且开口方向、形状与函数y=-2x2的图象相同的抛物线是（ ）
| A、y=-2（x-5）2 |
| B、y=-2（x+5）2 |
| C、y=2（x+5）2 |
| D、y=-2x2-5 |
如图，在⊙O中，弦AB∥CD，若∠ABC=36°，则∠BOD等于（ ）| A、18° | B、36° |
| C、54° | D、72° |
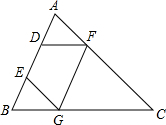如图，D、E是△ABC边AB上的点，F、G分别是边AC、BC上的点，且满足AD=DE=EB，DF∥BC，EG∥AC．