题目内容
已知二次函数y=x2—2x+c(c为常数).
(1)若该二次函数的图象与两坐标轴有三个不同的交点,求c的取值范围;
(2)已知该二次函数的图象与x轴交于点A(-1,0)和点B,与y轴交于点C,顶点为D,若存在点P(m,0)(m>3)使得△CDP与△BDP面积相等,求m的值.
解:(1)由题意可得,该二次函数与x轴有两个不同的交点,
也就是当y=0时,方程x2—2x+c=0有两个不相等的实数根,
即b2-4ac>0,所以4-4c>0,c<1.
又因为该二次函数与两个坐标轴有三个不同的交点,所以c≠0.
综上,若该二次函数的图象与两坐标轴有三个不同的交点,
c的取值范围为c<1且c≠0. 4分
(2)因为点A(-1,0)在该二次函数图象上,可得0=(-1)2-2×(-1)+c,c=-3.
所以该二次函数的关系式为y=x2—2x-3,可得C(0,-3).
由x=-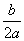 =1,可得B(3,0),D(1,-4).
=1,可得B(3,0),D(1,-4).
若点P(m,0)(m>3)使得△CDP与△BDP面积相等,
可得点C、B到DP的距离相等,此时,CB∥DP.
设过点C、B的直线的函数关系式为y=kx+b,即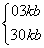 解得
解得
设过点D、P的直线的函数关系式为y=x+n,即-4=1+n.解得n=-5.
即y=x-5,当y=0时,x=5,即m=5. 9分

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案为了解南京市民每天的阅读时间情况,随机抽取了部分市民进行调查,根据调查结果绘制如下尚不完整的频数分布表:
| 阅读时间 x(min) | 0≤x<30 | 30≤x<60 | 60≤x<90 | x≥90 | 合计 |
| 频数 | 450 | 400 | ② | 50 | ④ |
| 频率 | ① | 0.4 | 0.1 | ③ | 1 |
(1)补全表格中①~④的数据;
(2)将每天阅读时间不低于60 min的市民称为“阅读爱好者”,若我市约有800万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?
△ABC中,AB=AC=10,BC=12,矩形DEFG中,EF=4,FG>12.
(1)如图①,点A是FG的中点,FG∥BC,将矩形DEFG向下平移,直到DE与BC重合为止.要研究矩形DEFG与△ABC重叠部分的面积,就要进行分类讨论,你认为如何进行分类,写出你的分类方法(无需求重叠部分的面积).
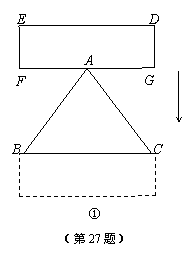 |
(2)如图②,点B与F重合,E、B、C在同一直线上,将矩形DEFG向右平移,直到点E与C重合为止.设矩形DEFG与△ABC重叠部分的面积为y,平移的距离为x.
① 求y与x的函数关系式,并写出自变量的取值范围;
② 在给定的平面直角坐标系中画出y与x的大致图象,并在图象上标注出关键点坐标.
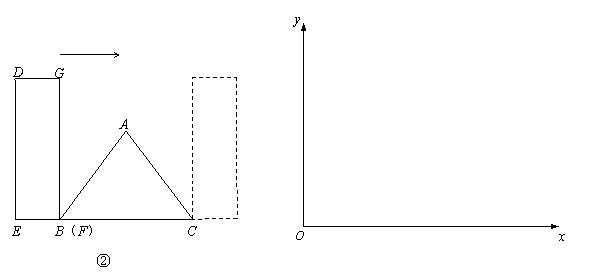 |
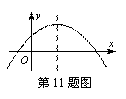 二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置
二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置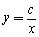 在同
在同 
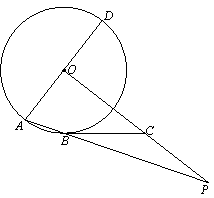
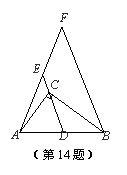

 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为 .
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为 .