题目内容
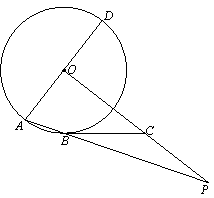
如图，AD是⊙O的直径，AB为⊙O 的弦，OP⊥AD，OP与AB的延长线交于点P．点C在OP上，且BC＝PC．
（1）求证：直线BC是⊙O的切线；
（2）若OA＝3，AB＝2，求BP的长．
 |
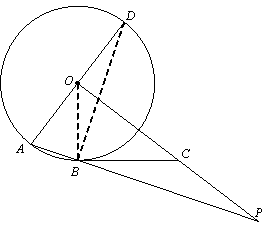
（1）证明：连结OB．
∵OA＝OB，∴∠A＝∠OBA．
又∵BC＝PC，∴∠P＝∠CBP． …………1分
∵OP⊥AD，∴∠A＋∠P＝90°，
∴∠OBA＋∠CBP＝90°，…………2分
∴∠OBC＝180°－（∠OBA＋∠CBP）＝90°．
∵点B在⊙O上，
∴直线BC是⊙O的切线． …………4分
（2）连结DB．
∵AD是⊙O的直径，∴∠ABD＝90°，
∴Rt△ABD∽Rt△AOP．…………6分
∴
＝
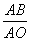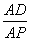，即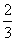 
＝
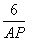，AP＝9，…………7分
∴BP ＝AP—BA＝9—2＝7． …………8分
练习册系列答案
相关题目
的解集在数轴上表示为（ ）
如图，△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D.
（1）求证：BE＝CF；
（2）当四边形ACDE为菱形时，求BD的长.
的长度为 ．
某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了
部分学生的听写结果，绘制成如下的图表．
|
根据以上信息完成下列问题：
（1）统计表中的m＝ ，n＝ ，并补全条形统计图；
（2）扇形统计图中“C组”所对应的圆心角的度数是 ；
（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，
请你估计该校本次听写比赛不合格的学生人数．
等于