题目内容
2.计算题:(1)(-2)-(+5)-(-3)+4
(2)-5-2+5-11+2
(3)(-3)×2+20÷(-5)
(4)$(\frac{3}{4}-\frac{1}{6}-\frac{5}{8})×(-24)$
(5)$(-\frac{3}{4})×(-\frac{1}{2})$÷$(-2\frac{1}{4})$
(6)$-3.5÷\frac{7}{8}×(-\frac{3}{4})$
(7)$({\frac{2}{3}-\frac{1}{12}-\frac{4}{15}})×({-60})$
(8)$({-1})-[{(-2)×({-4})+|{-\frac{1}{2}}|÷({-\frac{1}{4}})}]$.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式结合后,相加即可得到结果;
(3)原式先计算乘除运算,再计算加减运算即可得到结果;
(4)原式利用乘法分配律计算即可得到结果;
(5)原式从左到右依次计算即可得到结果;
(6)原式从左到右依次计算即可得到结果;
(7)原式利用乘法分配律计算即可得到结果;
(8)原式先计算中括号中的乘除运算,再计算加减运算即可得到结果.
解答 解:(1)原式=-2-5+3+4=-7+7=0;
(2)原式=-18+7=-11;
(3)原式=-6-4=-10;
(4)原式=-18+4+15=1;
(5)原式=-$\frac{3}{4}$×$\frac{1}{2}$×$\frac{4}{9}$=-$\frac{1}{6}$;
(6)原式=$\frac{7}{2}$×$\frac{8}{7}$×$\frac{3}{4}$=3;
(7)原式=-40+5+16=-40+21=-19;
(8)原式=-1-(8-2)=-1-6=-7.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为( )
如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为( )
 如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为( )
如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为( )| A. | 30 | B. | 15 | C. | 7.5 | D. | 45 |
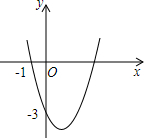 如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限.设m=a+b+c,则m的取值范围是-6<m<0.
如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限.设m=a+b+c,则m的取值范围是-6<m<0. 如图,已知AB=CD,AD=CB,且AB∥CD,AD∥BC,AC,BD相交于点O,则图中共有4对全等三角形.
如图,已知AB=CD,AD=CB,且AB∥CD,AD∥BC,AC,BD相交于点O,则图中共有4对全等三角形. 一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形的数字表示在该位置的小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形的数字表示在该位置的小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.