题目内容
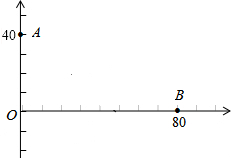 我海军某部发现,一艘敌舰从我岛屿O正东方向80海里的B处,沿东西方向向岛屿O驶来,指挥部立即下命令在岛屿O正北40海里A处的我军军舰沿直线前往拦截.若敌我两舰行驶速度相同,在上述坐标系中标出我舰最快截住敌舰的位置,并求出该点的坐标.
我海军某部发现,一艘敌舰从我岛屿O正东方向80海里的B处,沿东西方向向岛屿O驶来,指挥部立即下命令在岛屿O正北40海里A处的我军军舰沿直线前往拦截.若敌我两舰行驶速度相同,在上述坐标系中标出我舰最快截住敌舰的位置,并求出该点的坐标.考点:勾股定理的应用
专题:
分析:作出图形,根据题意可知,AC=BC,则OC=80-BC=80-AC,在Rt△AOC中,根据勾股定理得到AC2=OC2+OA2,解方程得到AC,进一步得到点的坐标.
解答: 解:如图,根据题意可知,AC=BC,
解:如图,根据题意可知,AC=BC,
则OC=80-BC=80-AC,
在Rt△AOC中,AC2=OC2+OA2,
则AC2=(80-AC)2+402,
解得AC=50,
则OC=80-AC=30,
则该点的坐标为(30,0).
 解:如图,根据题意可知,AC=BC,
解:如图,根据题意可知,AC=BC,则OC=80-BC=80-AC,
在Rt△AOC中,AC2=OC2+OA2,
则AC2=(80-AC)2+402,
解得AC=50,
则OC=80-AC=30,
则该点的坐标为(30,0).
点评:考查了勾股定理的应用,本题关键是作出图形,构造直角三角形,注意AC=BC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
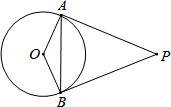 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=40°.则∠APB的度数为
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=40°.则∠APB的度数为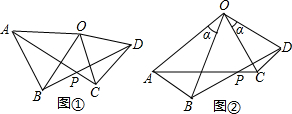
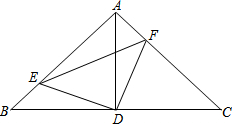 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.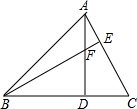 如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.
如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE. 如图,在正方形ABCD中,E为BC上的点,F为CD边上的点,且AE=AF,AB=4,设EC=x,△AEF的面积为y,则y与x之间的函数关系式是
如图,在正方形ABCD中,E为BC上的点,F为CD边上的点,且AE=AF,AB=4,设EC=x,△AEF的面积为y,则y与x之间的函数关系式是 已知D、E、F分别为△ABC的三边BC、CA、AB边上的一点,且CE=BF,S△DCE=S△DBF.求证:AD平分∠BAC.
已知D、E、F分别为△ABC的三边BC、CA、AB边上的一点,且CE=BF,S△DCE=S△DBF.求证:AD平分∠BAC.