题目内容
 如图,在正方形ABCD中,E为BC上的点,F为CD边上的点,且AE=AF,AB=4,设EC=x,△AEF的面积为y,则y与x之间的函数关系式是
如图,在正方形ABCD中,E为BC上的点,F为CD边上的点,且AE=AF,AB=4,设EC=x,△AEF的面积为y,则y与x之间的函数关系式是考点:正方形的性质,根据实际问题列二次函数关系式
专题:
分析:根据正方形的性质可得AB=AD,再利用“HL”证明Rt△ABE和Rt△ADF全等,根据全等三角形对应边相等可得BE=DF,然后求出CE=CF,再根据△AEF的面积等于正方形的面积减去三个直角三角形的面积列式整理即可得解.
解答:解:在正方形ABCD中,AB=AD,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,
∵CE=x,
∴BE=DF=4-x,
∴y=42-2×
×4×(4-x)-
x2,
=-
x2+4x,
即y=-
x2+4x.
故答案为:y=-
x2+4x.
在Rt△ABE和Rt△ADF中,
|
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,
∵CE=x,
∴BE=DF=4-x,
∴y=42-2×
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
即y=-
| 1 |
| 2 |
故答案为:y=-
| 1 |
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,三角形的面积,熟记性质并求出三角形全等是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图,该图形围绕自己的旋转中心,至少旋转多少度能与自身重合的是( )
如图,该图形围绕自己的旋转中心,至少旋转多少度能与自身重合的是( )| A、72° | B、144° |
| C、180° | D、360° |
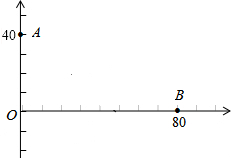 我海军某部发现,一艘敌舰从我岛屿O正东方向80海里的B处,沿东西方向向岛屿O驶来,指挥部立即下命令在岛屿O正北40海里A处的我军军舰沿直线前往拦截.若敌我两舰行驶速度相同,在上述坐标系中标出我舰最快截住敌舰的位置,并求出该点的坐标.
我海军某部发现,一艘敌舰从我岛屿O正东方向80海里的B处,沿东西方向向岛屿O驶来,指挥部立即下命令在岛屿O正北40海里A处的我军军舰沿直线前往拦截.若敌我两舰行驶速度相同,在上述坐标系中标出我舰最快截住敌舰的位置,并求出该点的坐标. 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,E为CD中点,已知AB=5,BE=6.5,求梯形的面积.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,E为CD中点,已知AB=5,BE=6.5,求梯形的面积. 八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,设直线l和八个正方形的最上面交点为A,则A的坐标是
八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,设直线l和八个正方形的最上面交点为A,则A的坐标是 如图,已知AB=AD,需要条件(用图中的字母表示)
如图,已知AB=AD,需要条件(用图中的字母表示)