题目内容
3. 如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
分析 根据抛物线形的拱桥在坐标系中的位置,找出抛物线上顶点和另一个点的坐标,代入抛物线的顶点式求出抛物线的解析式,再根据铁柱所在地的横坐标求出纵坐标,就是铁柱的高度.
解答 解:建立如图所示的坐标系,
抛物线的顶点坐标为(20,16),点B(40,0),
∴可设抛物线的关系为y=a(x-20)2+16.
∵点B(40,0)在抛物线上,
∴a(40-20)2+16=0,
∴a=-$\frac{1}{25}$.
∴y=-$\frac{1}{25}$(x-20)2+16.
∵竖立柱柱脚的点为(15,0)或(25,0),
∴当x=15时,y=-$\frac{1}{25}$(15-20)2+16=15m;
当x=25时,y=-$\frac{1}{25}$(25-20)2+16=15m.
∴铁柱应取15m.
点评 本题主要考查二次函数的应用,解题的关键建立合适的坐标系并选择适当的方法求出二次函数的解析式,运用解析式求出铁柱的高度.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
14.最简二次根式$\sqrt{4x-8}$与$\sqrt{32}$是同类二次根式,则x等于( )
| A. | $\frac{5}{2}$ | B. | 10 | C. | 2 | D. | 4 |
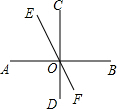 已知:AB⊥CD于O点,直线E过O点,∠EOC=15°,求∠BOF的度数.
已知:AB⊥CD于O点,直线E过O点,∠EOC=15°,求∠BOF的度数.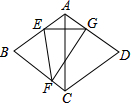 如图,在菱形ABCD中,∠BAD=120°,点E,F分别在AB,BC上,将△BEF沿EF折叠,点B落在AD上的点G处,EG⊥AC.
如图,在菱形ABCD中,∠BAD=120°,点E,F分别在AB,BC上,将△BEF沿EF折叠,点B落在AD上的点G处,EG⊥AC.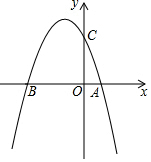 如图,已知抛物线y=-x2-2x+3与坐标轴分别交于A,B,C三点,在抛物线上找到一点D,使得∠DCB=∠ACO,则D点坐标为(-$\frac{5}{2}$,$\frac{7}{4}$)或(-4,-5).
如图,已知抛物线y=-x2-2x+3与坐标轴分别交于A,B,C三点,在抛物线上找到一点D,使得∠DCB=∠ACO,则D点坐标为(-$\frac{5}{2}$,$\frac{7}{4}$)或(-4,-5). 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.