题目内容
10.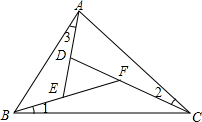 如图,在△ABC中,∠1=∠2=∠3,ED=2,AB=3,S△ABC=27.求S△DEF.
如图,在△ABC中,∠1=∠2=∠3,ED=2,AB=3,S△ABC=27.求S△DEF.
分析 由三角形的外角性质证出∠DFE=∠ACB,同理:∠DEF=∠ABC,得出△DEF∽△ABC,由相似三角形的面积比等于相似比的平方,即可得出结果.
解答 解:∵∠DFE=∠BCF+∠1,ACB=∠BCF+∠3,∠1=∠3,
∴∠DFE=∠ACB,
同理:∠DEF=∠ABC,
∴△DEF∽△ABC.
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{DE}{AB}$)2=($\frac{2}{3}$)2=$\frac{4}{9}$,
∴S△DEF=$\frac{4}{9}$S△ABC=$\frac{4}{9}$×27=12.
点评 本题考查了相似三角形的判定与性质、三角形的外角性质;熟练掌握相似三角形的判定与性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | a3-a2=a | B. | a2•a3=a6 | C. | (-3a)3=-9a3 | D. | (-a3)2=a6 |
18.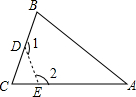 如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
 如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )| A. | 240° | B. | 120° | C. | 230° | D. | 200° |
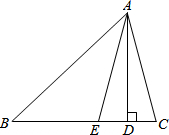 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=45°,∠C=75°,求∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=45°,∠C=75°,求∠DAE的度数. 如图,有一块扇形土地,现将平均分给甲、乙两户人家应如何分?(不写作法,保留作图痕迹)
如图,有一块扇形土地,现将平均分给甲、乙两户人家应如何分?(不写作法,保留作图痕迹)
 如图,反比例函数y=$\frac{k}{x}$的图象经过点(5,4),若y>4,则x的取值范围是0<x<5.
如图,反比例函数y=$\frac{k}{x}$的图象经过点(5,4),若y>4,则x的取值范围是0<x<5.