题目内容
20. 如图,九年级某班数学兴趣小组利用数学活动课时间测量位于铁人纪念馆台阶顶部铁人雕像的高度,已知台阶坡面与水平面的夹角∠BDC=30°,台阶总高BC=5m,组员从台阶底部D处沿台阶前行8m到达E点,在点E处测得雕像顶端A的仰角为60°,则雕像AB的高度为2m.
如图,九年级某班数学兴趣小组利用数学活动课时间测量位于铁人纪念馆台阶顶部铁人雕像的高度,已知台阶坡面与水平面的夹角∠BDC=30°,台阶总高BC=5m,组员从台阶底部D处沿台阶前行8m到达E点,在点E处测得雕像顶端A的仰角为60°,则雕像AB的高度为2m.
分析 构造直角三角形,利用锐角三角函数,进行简单计算即可.
解答 
过点E作EF⊥AC,EG⊥CD,
在Rt△DEG中,
∵DE=1620,∠D=30°,
∴EG=DEsin∠D=8×$\frac{1}{2}$=4米,
∵BC=5米,CF=EG,
∴BF=BC-CF=1米,
在Rt△BEF中,tan∠BEF=$\frac{BF}{EF}$,
∴EF=$\sqrt{3}$BF,
在Rt△AEF中,∠AEF=60°,设AB=x,
∵tan∠AEF=$\frac{AF}{EF}$,
∴AF=EF×tan∠AEF,
∴x+1=3×1,
∴x=2,
故答案为2.
点评 本题考查了解直角三角形-仰角俯角问题,主要考查了锐角三角函数的意义,解本题的关键是构造直角三角形.

练习册系列答案
相关题目
15. 如图,点P为正方形ABCD内一点,从①PA=PB;②∠PAB=15°;③∠ADP=30°三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,命题正确的个数为( )
如图,点P为正方形ABCD内一点,从①PA=PB;②∠PAB=15°;③∠ADP=30°三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,命题正确的个数为( )
 如图,点P为正方形ABCD内一点,从①PA=PB;②∠PAB=15°;③∠ADP=30°三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,命题正确的个数为( )
如图,点P为正方形ABCD内一点,从①PA=PB;②∠PAB=15°;③∠ADP=30°三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,命题正确的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.下列代数运算正确的是( )
| A. | (x3)2=x5 | B. | (3x)2=3x2 | C. | x3•x2=x5 | D. | (x-1)2=x2-1 |
 如图,△ABC中,点D在边BC上,DE⊥AB于E,DH⊥AC于H,且满足DE=DH,F为AE的中点,G为直线AC上一动点,满足DG=DF.若AE=4cm,则AG=2或6cm.
如图,△ABC中,点D在边BC上,DE⊥AB于E,DH⊥AC于H,且满足DE=DH,F为AE的中点,G为直线AC上一动点,满足DG=DF.若AE=4cm,则AG=2或6cm.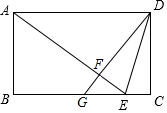 如图,矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE于点F,延长DF交BC于点G,连接DE.
如图,矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE于点F,延长DF交BC于点G,连接DE. 甲、乙两车从A地出发匀速行驶至B地,在整个行驶过程中,甲、乙两车离开A地的距离y1(单位:km),y2(单位:km)关于甲车行驶的时间t(单位:h)的函数关系如图所示,根据图象解答下列问题:
甲、乙两车从A地出发匀速行驶至B地,在整个行驶过程中,甲、乙两车离开A地的距离y1(单位:km),y2(单位:km)关于甲车行驶的时间t(单位:h)的函数关系如图所示,根据图象解答下列问题: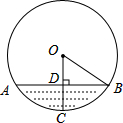 在直径为150cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度DC为30cm,那么油面宽度AB是120cm.
在直径为150cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度DC为30cm,那么油面宽度AB是120cm.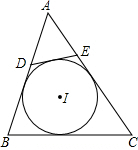 如图,⊙I为△ABC的内切圆,D、E分别为边AB、AC上的点,且DE为⊙I的切线,若△ABC的周长为19,BC边的长为5,则△ADE的周长为9.
如图,⊙I为△ABC的内切圆,D、E分别为边AB、AC上的点,且DE为⊙I的切线,若△ABC的周长为19,BC边的长为5,则△ADE的周长为9.