题目内容
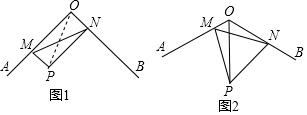
15. 如图,点P为正方形ABCD内一点,从①PA=PB;②∠PAB=15°;③∠ADP=30°三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,命题正确的个数为( )
如图,点P为正方形ABCD内一点,从①PA=PB;②∠PAB=15°;③∠ADP=30°三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,命题正确的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①②⇒③是真命题,①③⇒②是真命题,②③⇒①是真命题,由此即可判断.
解答 解:①②⇒③是真命题, 理由:作PF⊥AB于F,PE⊥AD于E,
理由:作PF⊥AB于F,PE⊥AD于E,
当△PDC是等边三角形时,①②条件成立,
易证PE=AF=$\frac{1}{2}$AB=$\frac{1}{2}$DC=$\frac{1}{2}$PD,可得∠ADP=30°
①③⇒②是真命题,
理由:首先证明△PDC是等边三角形,推出DA=DP,推出∠DAP=75°,可得结论.
②③⇒①是真命题,
理由:首先证明:DA=DP,△PDC是等边三角形,即可推出结论.
故选D.
点评 本题考查命题与定理、正方形的性质、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
3.实数a,b,c满足a<b<0<c,则下列式子中正确的是( )
| A. | ac>bc | B. | |a-b|=a-b | C. | -a<-b<c | D. | -a-c>-b-c |
10. 实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
 实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )| A. | a>-2 | B. | a<-3 | C. | -a<b | D. | a<-b |
 如图,九年级某班数学兴趣小组利用数学活动课时间测量位于铁人纪念馆台阶顶部铁人雕像的高度,已知台阶坡面与水平面的夹角∠BDC=30°,台阶总高BC=5m,组员从台阶底部D处沿台阶前行8m到达E点,在点E处测得雕像顶端A的仰角为60°,则雕像AB的高度为2m.
如图,九年级某班数学兴趣小组利用数学活动课时间测量位于铁人纪念馆台阶顶部铁人雕像的高度,已知台阶坡面与水平面的夹角∠BDC=30°,台阶总高BC=5m,组员从台阶底部D处沿台阶前行8m到达E点,在点E处测得雕像顶端A的仰角为60°,则雕像AB的高度为2m.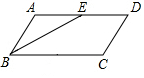 如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是12.
如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是12.