题目内容
关于x的方程x2+2kx+k-1=0的根的情况描述正确的是( )
| A、k为任何实数,方程都有实根 |
| B、k为任何实数,方程都有两个不相等的实根 |
| C、k为任何实数,方程都有两个相等的实根 |
| D、以上说法都对 |
考点:根的判别式
专题:计算题
分析:先计算判别式的值得到△=(2k-1)2+3,根据非负数的性质得△>0,然后根据判别式的意义进行判断.
解答:解:△=4k2-4(k-1)
=(2k-1)2+3,
∵4(k-1)2≥0,
∴(2k-1)2+3>0
即△>0,
∴方程有两个不相等的实数根.
故选B.
=(2k-1)2+3,
∵4(k-1)2≥0,
∴(2k-1)2+3>0
即△>0,
∴方程有两个不相等的实数根.
故选B.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
 如图,等腰△ABC的底角为30°,底边上的高AD=5,则腰AB、AC的值为( )
如图,等腰△ABC的底角为30°,底边上的高AD=5,则腰AB、AC的值为( )| A、20 | B、15 | C、10 | D、7.5 |
已知2+
是关于x的方程x2-4x+c=0的一根,则c的值是( )
| 3 |
| A、-1 | B、0 | C、1 | D、2 |
方程x(x-1)=0的解是( )
| A、x1=0,x2=1 |
| B、x1=0,x2=-1 |
| C、x1=0,x2=0 |
| D、x1=x2=1 |
大于-2.5而小于
的整数共有( )
| 5 |
| A、6个 | B、5个 | C、4个 | D、3个 |
若分式
的值为零,那么x的值为( )
| x2-1 |
| x+1 |
| A、x=1或x=-1 | B、x=1 |
| C、x=-1 | D、x=0 |
不能进行密铺的图形是( )
| A、正三边形 | B、正四边形 |
| C、正五边形 | D、正六边形 |
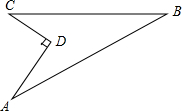 如图,已知AD=4,CD=3,∠ADC=90°,AB=13,BC=12.
如图,已知AD=4,CD=3,∠ADC=90°,AB=13,BC=12. 如图,四边形ABCD是平行四边形,点E、F分别在BD上,且BE=DF.
如图,四边形ABCD是平行四边形,点E、F分别在BD上,且BE=DF.